Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Déterminer la médiane, le 1er quartile et le 3ème quartile - Exercice 1
20 min
35
Un entraineur d'une équipe d'handball fait le bilan du nombre de buts inscrits par match lors de la saison -.
Pour chaque match, il a noté le nombre de buts inscrits. Il obtient les résultats suivants :

Pour chaque match, il a noté le nombre de buts inscrits. Il obtient les résultats suivants :

Question 1
Calculer le er quartile.
Correction
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
On va commencer par définir les effectifs cumulés croissants (ECC).

Pour déterminer le er quartile, on commence par calculer ce qui donne .
Le er quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à buts)
Question 2
Calculer le ème quartile.
Correction
On reprend le tableau des effectifs cumulés croissants.

Pour déterminer le ème quartile, on commence par calculer ce qui donne .
Le ème quartile, noté , correspond à la ème valeur de la série ordonnée ( on arrondi toujours par excès si son écriture est décimal).
Ainsi :
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à buts)

Pour déterminer le ème quartile, on commence par calculer ce qui donne .
Le ème quartile, noté , correspond à la ème valeur de la série ordonnée ( on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à buts)
Question 3
Calculer la médiane.
Correction
On reprend le tableau des effectifs cumulés croissants.

Pour déterminer la médiane, on commence par calculer ce qui donne .
La médiane, notée , correspond à la ème valeur de la série ordonnée (ici, nous avons un effectif total impair et dans ce cas on arrondi toujours par excès si son écriture est décimal).
Ainsi :
(Dans la ligne des ECC on recherche la valeur , ici apparaît et donc cela correspond à buts).

Pour déterminer la médiane, on commence par calculer ce qui donne .
La médiane, notée , correspond à la ème valeur de la série ordonnée (ici, nous avons un effectif total impair et dans ce cas on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur , ici apparaît et donc cela correspond à buts).
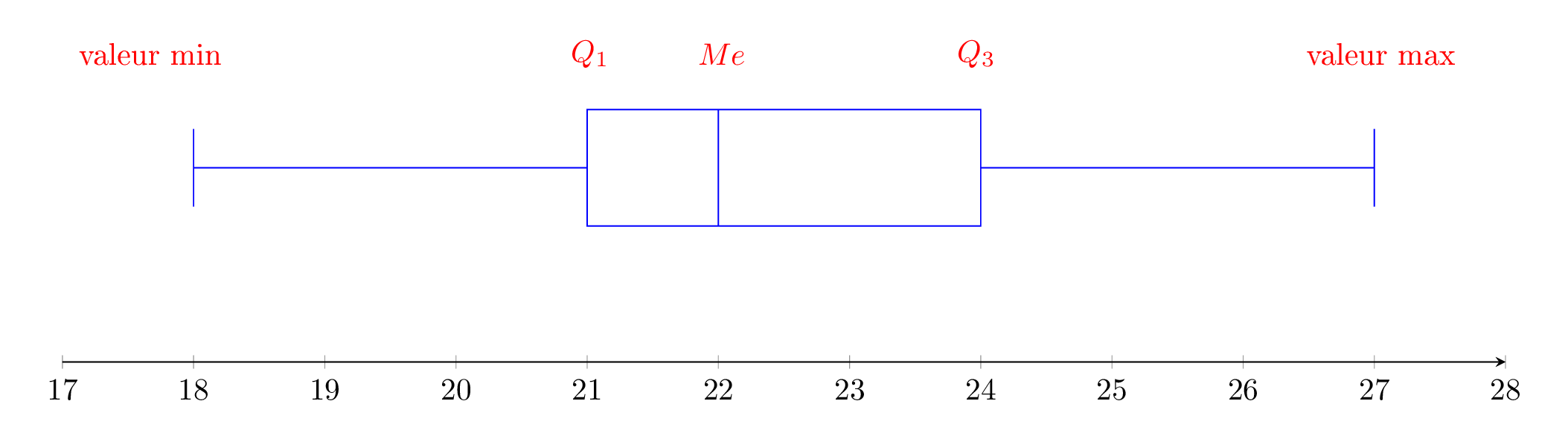
Question 4
Construire la boite à moustaches de cette série.
Correction