Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
15 min
30
On a placé dans une urne des boules de couleurs et numérotées. Les boules sont indiscernables au toucher.
On donne ci-dessous le nombre des boules selon leur couleur et le numéro qu'elles portent.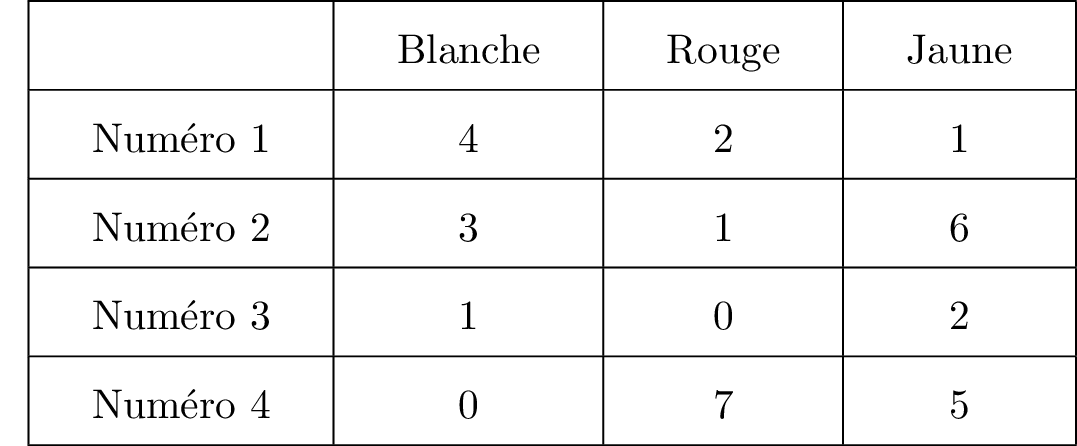
On donne ci-dessous le nombre des boules selon leur couleur et le numéro qu'elles portent.

Question 1
On prélève un jeton au hasard.
On considère les évènements suivants :
On considère les évènements suivants :
- : " La boule est jaune ".
- : " La boule est blanche ".
- : " La boule porte un numéro pair ".
Décrire par une phrase les évènements ; et .
Correction
Question 2
Calculer
Correction
Nous avons vu précédemment que l'évènement correspond à l'évènement : la boule est jaune porte un numéro pair .
Dans un premier temps, nous allons compléter le tableau avec les lignes indiquant les totaux.
Il vient :
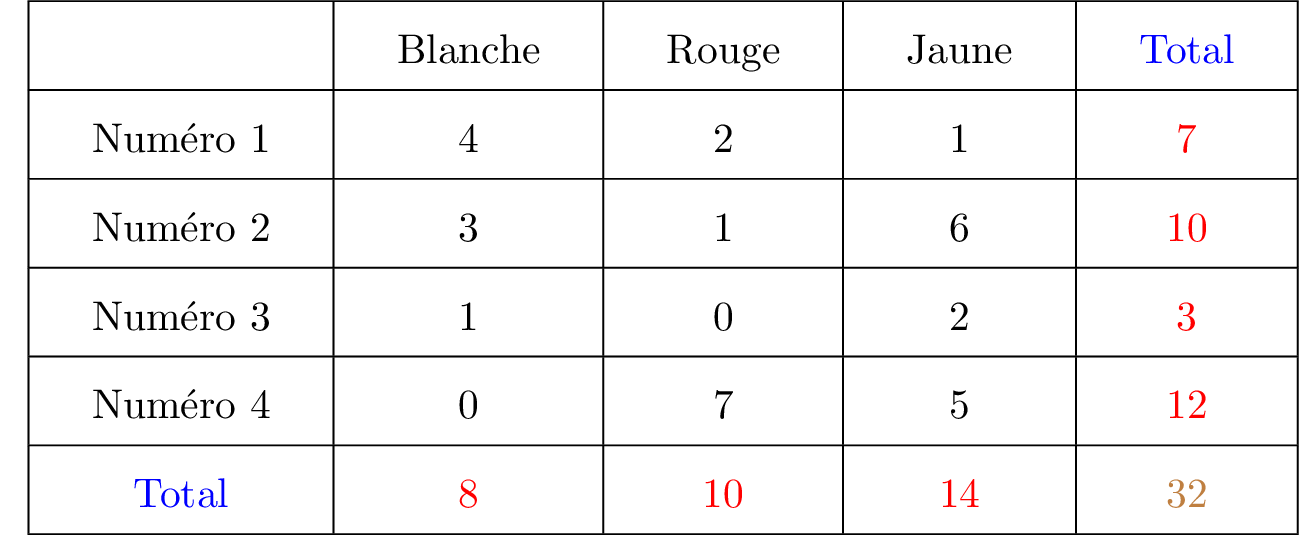 D'après ce tableau, nous avons boules jaunes numérotées et boules jaunes numérotées .
D'après ce tableau, nous avons boules jaunes numérotées et boules jaunes numérotées .
Il en résulte donc que :
Dans un premier temps, nous allons compléter le tableau avec les lignes indiquant les totaux.
Il vient :

Il en résulte donc que :
Question 3
Calculer et
Correction
Nous savons que :  Soient les évènements suivants :
Soient les évènements suivants :

- : " La boule est jaune ".
- : " La boule porte un numéro pair ".
Question 4
Calculer
Correction
Pour tous évènements et , on a :
