Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 4
20 min
40
Toujours une histoire de Bac.
Une section de seconde comporte élèves. On donne les informations suivantes :
Une section de seconde comporte élèves. On donne les informations suivantes :
Question 1
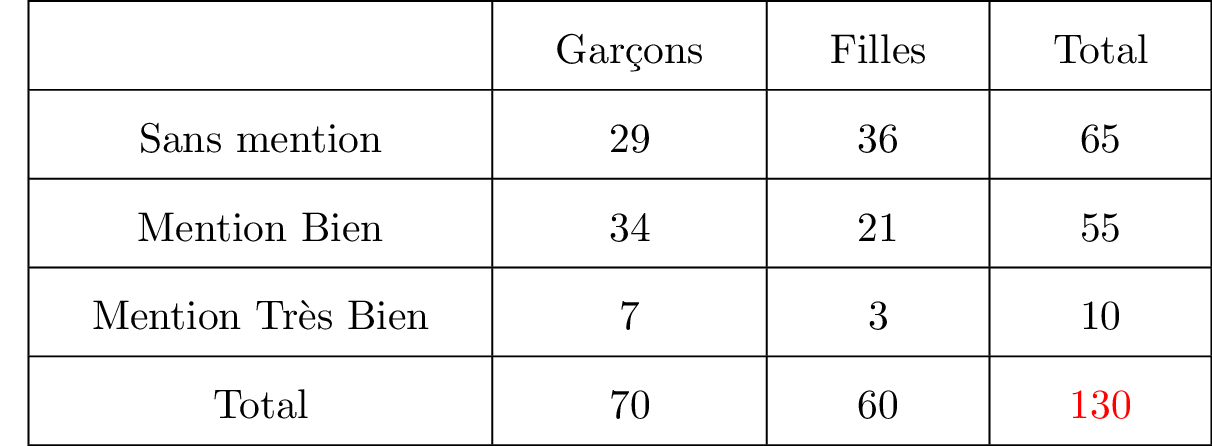
- l'événement : « avoir le bac sans mention »
- l'événement : « avoir le bac avec mention bien »
- l'événement : « avoir le bac avec mention très bien »
- l'événement : « être une fille »
Calculer la probabilité de l'évènement .
Correction

Question 2
Calculer la probabilité de l'évènement .
Correction

Question 3
Définir par une phrase l'évènement . Calculer la probabilité de cet évènement.
Correction

Question 4
Définir par une phrase l'évènement . Calculer la probabilité de cet évènement.
Correction

Question 5
La personne a eu un bac mention bien. Quelle est la probabilité que la personne soit un garçon. On notera cet évènement .
Correction
