Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 11ère partie - Exercice 3

20 min
40
Un lycée international permet de passer 33 différents baccalauréats.
  • Le bac classique Français
  • Le bac américain appelé "A Levels"
  • Le bac italien appelé "Maturita"
    • On dénombre les effectifs suivants :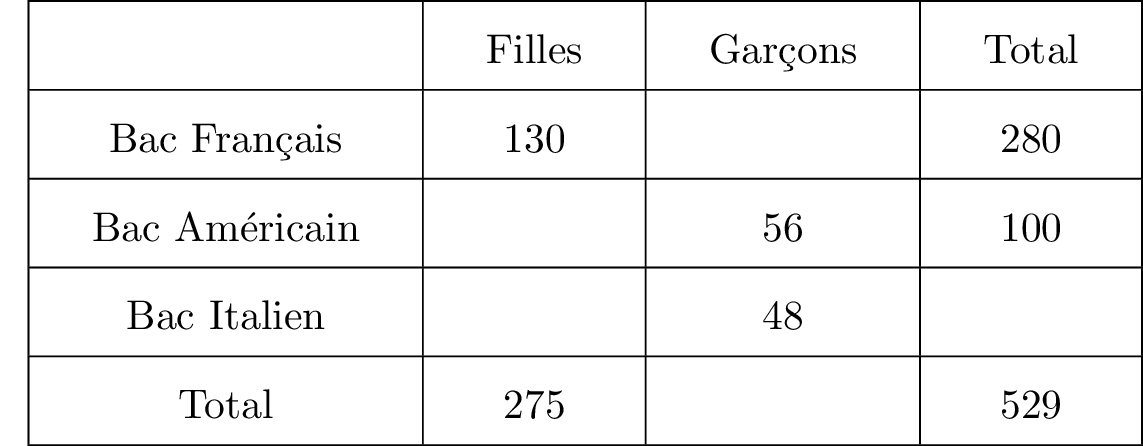
    Question 1
    On note :
    • AA l'événement : « passer le bac Français »
    • LL l'événement : « passer le bac Américain »
    • II l'événement : « passer le bac italien »
    • FF l'événement : « être une fille »

    Compléter le tableau ci-dessus.

    Correction
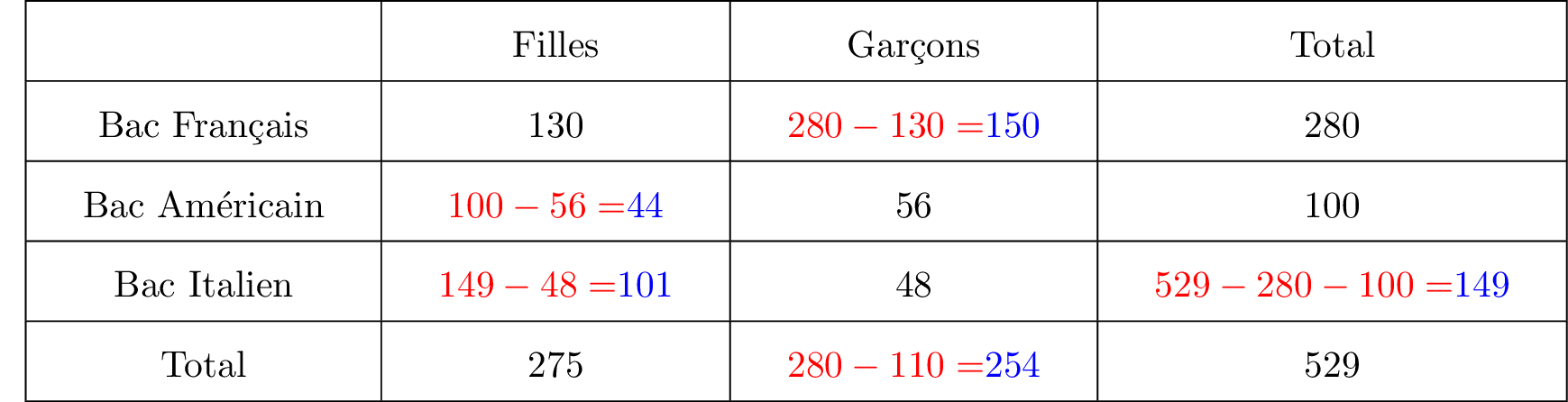
    Question 2

    Calculer la probabilité de l'évènement II.

    Correction
    p(I)=nombre des issues favorables pour Inombre des issues possiblesp\left(I\right)=\frac{\text{nombre des issues favorables pour }I}{\text{nombre des issues possibles}}
    p(I)=149529p\left(I\right)=\frac{149}{529}

    Question 3

    Calculer la probabilité de l'évènement FF.

    Correction
    p(F)=nombre des issues favorables pour Fnombre des issues possiblesp\left(F\right)=\frac{\text{nombre des issues favorables pour }F}{\text{nombre des issues possibles}}
    p(F)=275529p\left(F\right)=\frac{275}{529}

    Question 4

    Définir par une phrase l'évènement F∩IF\cap I. Calculer la probabilité de cet évènement.

    Correction
    F∩IF\cap I l'événement : « être une fille et passer le bac italien».
    p(F∩I)=nombre des issues favorables pour F∩Inombre des issues possiblesp\left(F\cap I\right)=\frac{\text{nombre des issues favorables pour }F\cap I}{\text{nombre des issues possibles}}
    p(F∩I)=101529p\left(F\cap I\right)=\frac{101}{529}
    Question 5

    Définir par une phrase l'évènement F∪IF\cup I. Calculer la probabilité de cet évènement.

    Correction
    F∪IF\cup I l'événement : « être une fille ou passer le bac italien».
    • P(A∪B)=P(A)+P(B)−P(A∩B)P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)
    P(F∪I)=P(F)+P(I)−P(F∩I)P\left(F\cup I\right)=P\left(F\right)+P\left(I\right)-P\left(F\cap I\right) équivaut successivement à :
    P(F∪I)=275529+149529−101529P\left(F\cup I\right)=\frac{275}{529}+\frac{149}{529}-\frac{101}{529}
    P(F∪I)=323529P\left(F\cup I\right)=\frac{323}{529}
    Question 6

    La personne passe un bac américain. Quelle est la probabilité que la personne soit un garçon. On notera MM cet évènement .

    Correction
    p(M)=nombre des issues favorables pour Mnombre des issues possiblesp\left(M\right)=\frac{\text{nombre des issues favorables pour }M}{\text{nombre des issues possibles}}
    p(M)=56100p\left(M\right)=\frac{56}{100}
    p(M)=1425p\left(M\right)=\frac{14}{25}