Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 1

10 min
20
Voici quatre droites tracées dans un repère orthonormal. Donner l’expression de chacune des fonctions associées à ces 44 droites
Question 1

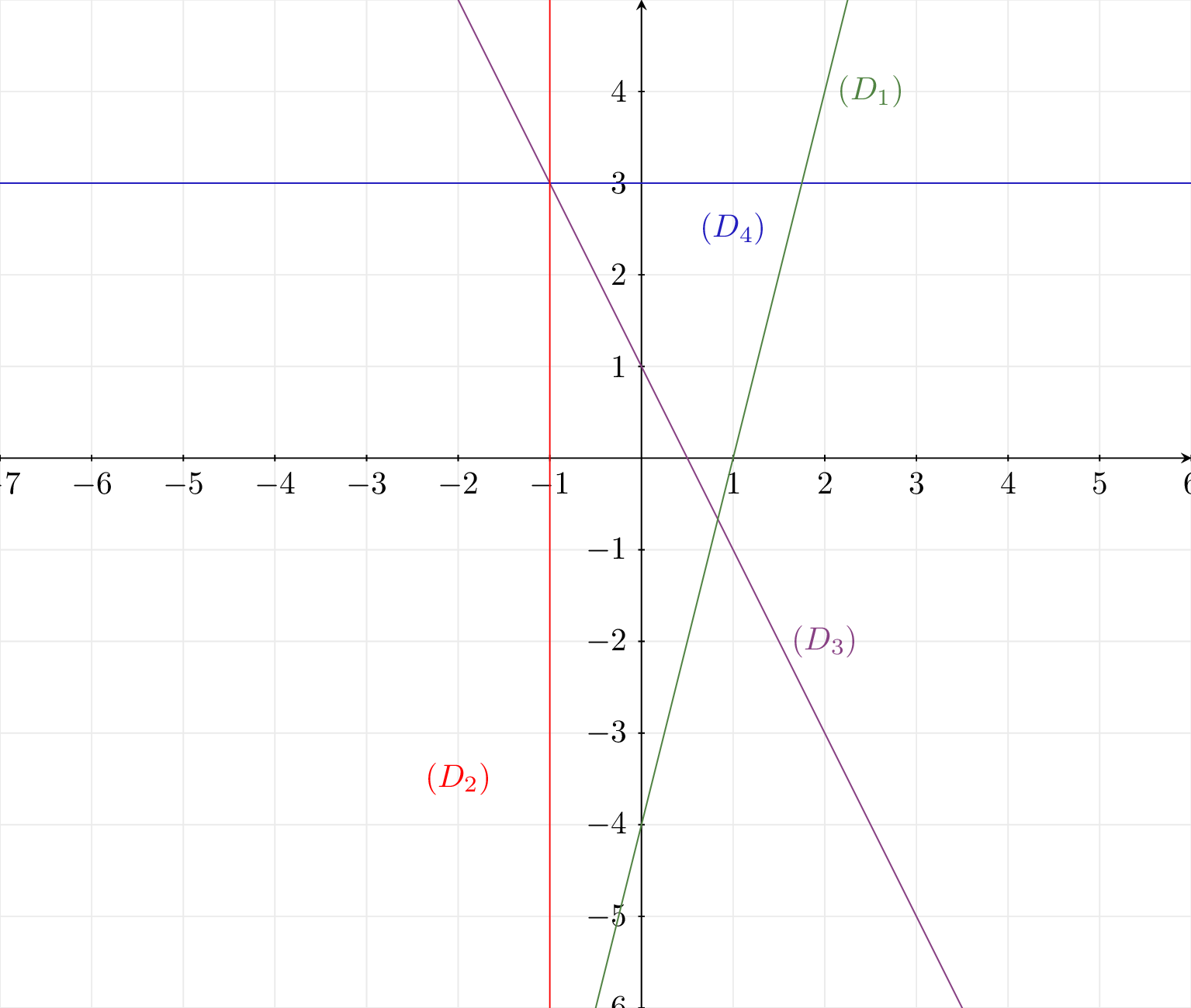
Correction
  • La droite (D1)\left(D_{1}\right) est une fonction affine de la forme y=ax+by=ax+b . L'ordonnée à l'origine bb est le point d'intersection entre l'axe des ordonnées et la droite (D1)\left(D_{1}\right). Nous pouvons facilement lire ici que
    b=−4b=-4
    .
    Pour déterminer le coefficient directeur de la droite (D1)\left(D_{1}\right), nous remarquons que les points A(0;−4)A\left(0;-4\right) et B(1;0)B\left(1;0\right) appartiennent à la droite (D1)\left(D_{1}\right). Nous pouvons donc calculer le coefficient directeur de la droite (D1)\left(D_{1}\right) à l'aide de la formule suivante :
    a=yB−yAxB−xA=0−(−4)1−0=4a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{0-\left(-4\right)}{1-0 }=4 . Finalement, la fonction affine associée à la droite (D1)\left(D_{1}\right) est de la forme :
    y=4x−4y=4x-4
  • La droite (D3)\left(D_{3}\right) est une fonction affine de la forme y=ax+by=ax+b . L'ordonnée à l'origine bb est le point d'intersection entre l'axe des ordonnées et la droite (D1)\left(D_{1}\right). Nous pouvons facilement lire ici que
    b=1b=1
    .
    Pour déterminer le coefficient directeur de la droite (D3)\left(D_{3}\right), nous remarquons que les points C(0;1)C\left(0;1\right) et D(2;−3)D\left(2;-3\right) appartiennent à la droite (D3)\left(D_{3}\right). Nous pouvons donc calculer le coefficient directeur de la droite (D3)\left(D_{3}\right) à l'aide de la formule suivante :
    a=yD−yCxD−xC=−3−12−0=−2a=\frac{y_{D}-y_{C}}{x_{D}-x_{C}}=\frac{-3-1}{2-0 }=-2 . Finalement, la fonction affine associée à la droite (D3)\left(D_{3}\right) est de la forme :
    y=−2x+1y=-2x+1
  • Une droite parallèle à l’axe des ordonnées ou verticale n’a pas de coefficient directeur. Ce qui signifie que tous les points de la droite (D2)\left(D_{2}\right) ont la même abscisse
    x=−1x =-1
    .
  • Une droite parallèle à l'axe des abscisses est horizontale et est donc de pente nulle. Donc, son coefficient directeur est nul : a=0a = 0. Ce qui signifie que tous les points de la droite (D4)\left(D_{4}\right) ont la même ordonnée
    y=3y =3
    .