Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
- Tous les niveaux>
- Seconde>
- Fonctions affines. Tableaux de signes . Inéquations produit et Inéquations quotient
Exercices types : ère partie - Exercice 1
15 min
25
Question 1
Tracer dans un repère les droites et d'équations et .
Correction
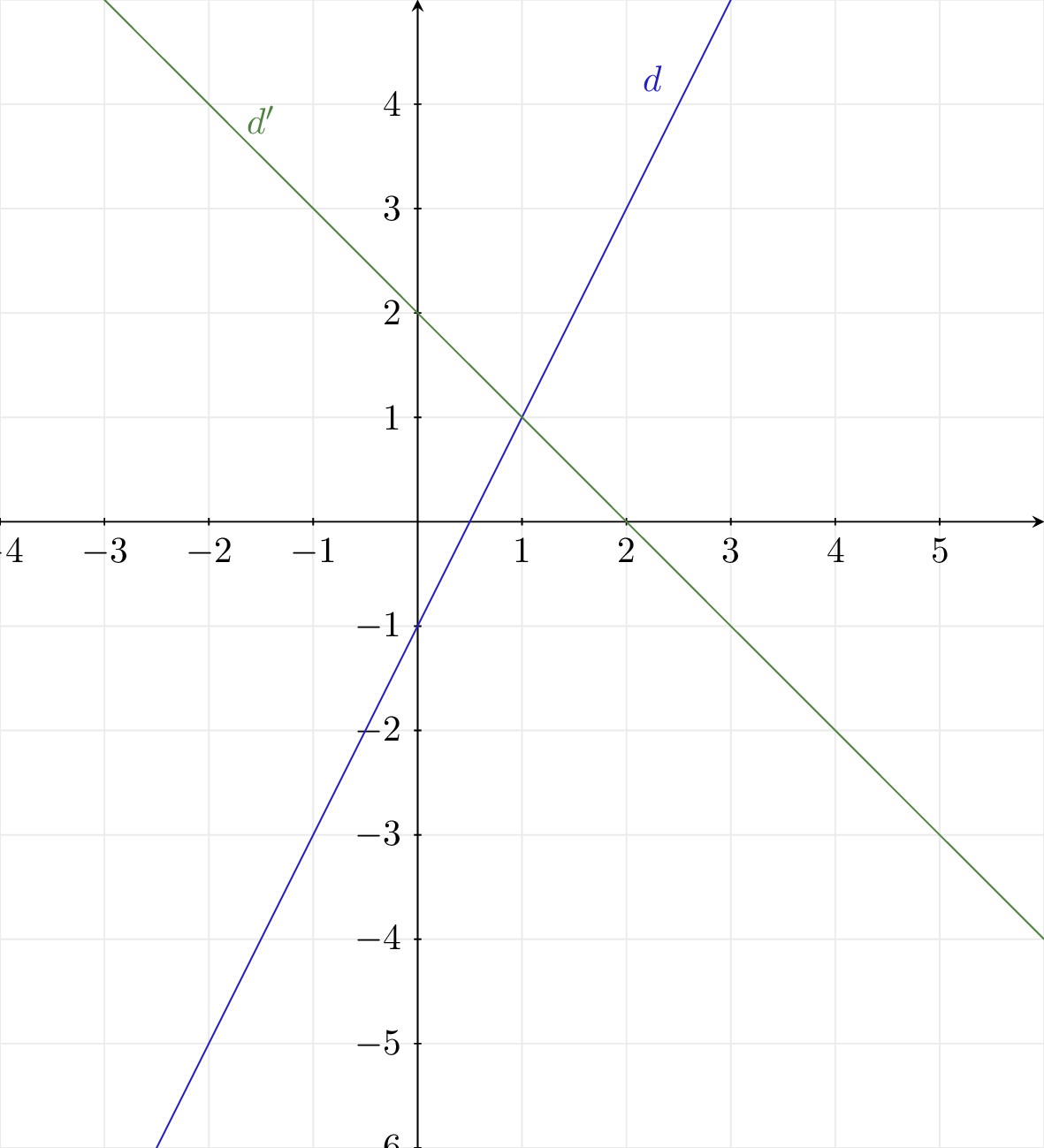
Question 2
Le point appartient-il à la droite ?
Correction
Le point appartient à la droite si et seulement si .
Soit :
Finalement, le point appartient bien à la droite ?
Soit :
Finalement, le point appartient bien à la droite ?
Question 3
Déterminer une équation de la droite parallèles à passant par le point .
Correction
- Deux droites sont parallèles si et seulement si les droites ont le même coefficient directeur.
La droite recherchée a comme équation et nous savons que et sont parallèles. Il en résulte donc que .
Ainsi :
Nous savons que le point appartient à la droite recherchée. Cela signifie donc que .
Il vient alors que :
équivaut successivement à :
Finalement, l'expression de la droite parallèles à passant par le point est :
Question 4
Montrer que les droites et sont sécantes, puis calculer les coordonnées de leur point d'intersection.
Correction
- Deux droites sont parallèles si et seulement si les droites ont le même coefficient directeur.
On vérifie aisément que les droites n'ont pas le même coefficient directeur car le coefficient directeur de la droite vaut alors que celui de la droite vaut . Il nous faut donc résoudre un système de deux équations à deux inconnues pour déterminer les cordonnées du point d'intersection entre et .
. Nous allons remplacer le de la deuxième ligne par la valeur du de la première ligne, ce qui donne :
. On obtient ainsi à la deuxième ligne une équation du premier degré que nous allons résoudre.
. Maintenant que nous avons trouver la valeur de l'abscisse du point d'intersection entre les deux droites, nous remplaçons cette valeur dans la première ligne du système afin d'obtenir l'ordonnée .
Les coordonnées du point d'intersection entre les droites et est le point que l'on note