Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
- Tous les niveaux>
- Seconde>
- Fonction de référence : La fonction racine carrée $f\left(x\right)=\sqrt{x}$
Résolution graphique - Exercice 2
15 min
25
Question 1
A l'aide de la représentation de la fonction carré, résoudre graphiquement les inéquations suivantes :
Correction
Sur le graphique ci-dessus, nous avons tracé la droite et la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont au dessus ou sur la droite d'équation et qui sont en dessous ou sur la droite .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire 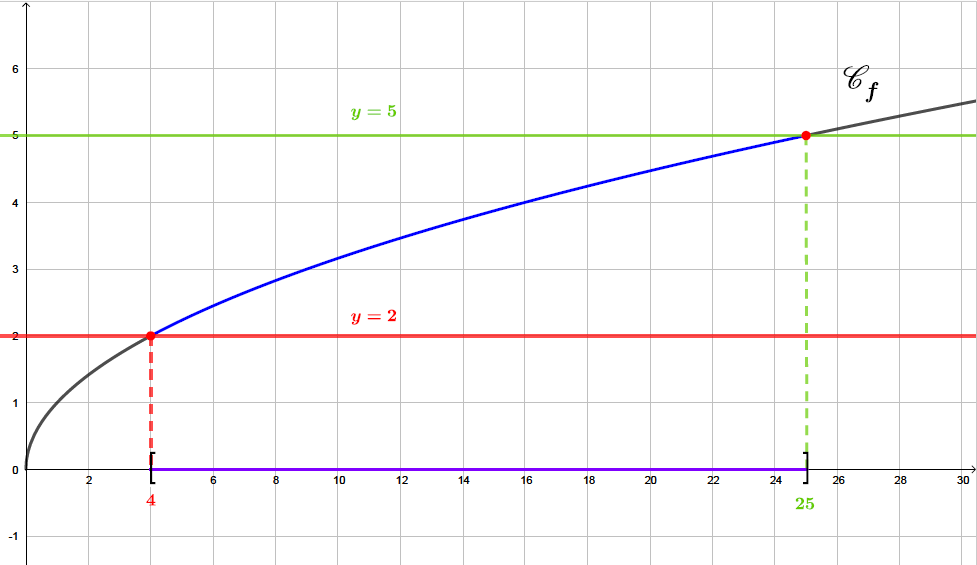
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire

Question 2
Correction
Sur le graphique ci-dessus, nous avons tracé la droite et la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont au dessus ou sur la droite d'équation et qui sont en dessous ou sur la droite .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire 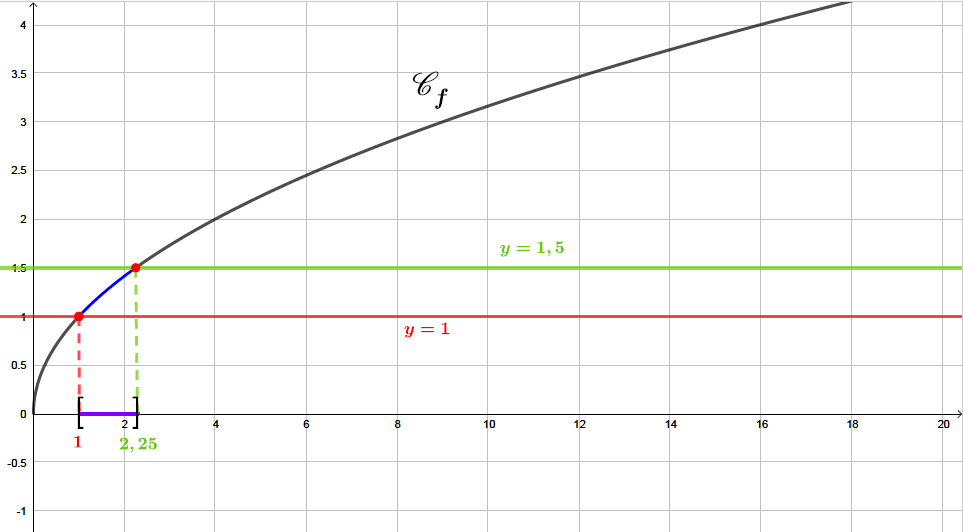
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire

Question 3
Correction
Sur le graphique ci-dessus, nous avons tracé la droite et la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont au dessus ou sur la droite d'équation et qui sont en dessous ou sur la droite .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire 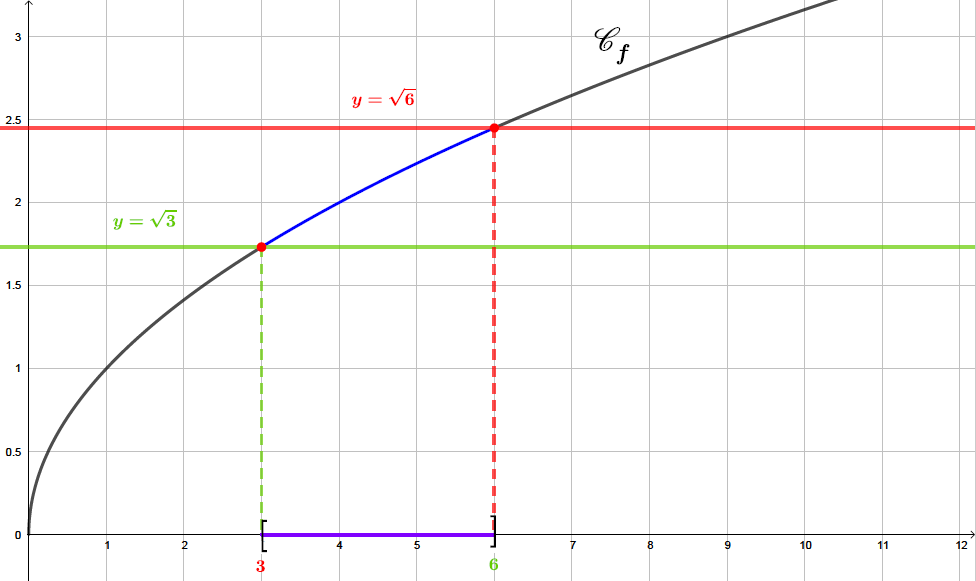
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : c'est à dire
