Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 1 ère partie : avec les racines carrées - Exercice 2

5 min
20
Soit ABCABC un triangle.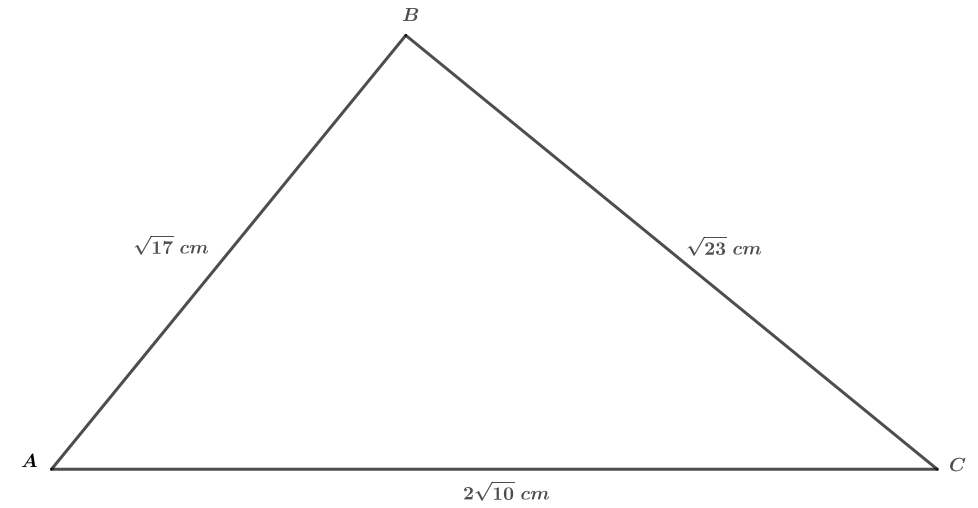
Question 1

Quelle est la nature du triangle ABCABC ?

Correction
    Soit aa un réel positif .
  • a2=a\sqrt{a^{2} } =a
  • Soient aa un réel positif et bb un réel alors : (ba)2=(b)2×(a)2\left(b\sqrt{a} \right)^{2} =\left(b\right)^{2} \times \left(\sqrt{a} \right)^{2}
Dans le triangle ABCABC, le plus grand côté est AC=210AC=2\sqrt{10} cm .
  • Calculons d'une part :
    • AC2=(210)2AC^{2} =\left(2\sqrt{10}\right)^{2}
    AC2=(2)2×(10)2AC^{2} =\left(2\right)^{2}\times\left(\sqrt{10}\right)^{2}
    AC2=4×10AC^{2} =4\times10
    AC2=40AC^{2} =40
  • Calculons d'autre part :
    • BA2+BC2=(17)2+(23)2BA^{2} +BC^{2} =\left(\sqrt{17}\right)^{2}+\left(\sqrt{23}\right)^{2}
    BA2+BC2=17+23BA^{2} +BC^{2} =17+23
    BA2+BC2=40BA^{2} +BC^{2}=40

    Or AC2=BA2+BC2{\color{blue}AC^{2}=BA^{2} +BC^{2}}
    Donc, d'après la réciproque du théorème de Pythagore le triangle ABCABC est rectangle en BB .