QCM Bilan 1 - Exercice 1

$$\red{\text{La bonne réponse est}}$$ $$\red{c}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, méthode \,\, de \,\, l'expression \,\,conjuguée}}}$$
Par la méthode de l'expression conjuguée, on trouve que :
$$\lim_{x \longrightarrow -\infty} \dfrac{\sqrt{x^2 + x} - \sqrt{x^2 + 1}}{\sqrt{3x^2 + 2x} - \sqrt{3x^2 + x + 1}} = \lim_{x \longrightarrow -\infty} \dfrac{\sqrt{3 + \dfrac{2}{x}} + \sqrt{3 + \dfrac{1}{x} + \dfrac{1}{x^2}}}{\sqrt{1 + \dfrac{1}{x}} +\sqrt{1 + \dfrac{1}{x^2}}} = \dfrac{ \sqrt{3} + \sqrt{3}}{\sqrt{1} + \sqrt{1}} = \dfrac{2\sqrt{3}}{2} = \sqrt{3}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{b}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, une \,\, factorisation \,\, et \,\, la \,\, méthode \,\, de \,\, l'expression \,\,conjuguée}}}$$
En effet, on a :
$$\lim_{x \longrightarrow 4} \dfrac{\sqrt{x} - 2}{x^2 - 5x + 4} = \lim_{x \longrightarrow 4} \dfrac{\sqrt{x} - 2}{(x-1)(x-4)} = \lim_{x \longrightarrow 4} \dfrac{\sqrt{x} - 2}{(x-1)(x-4)} \times \dfrac{\sqrt{x} + 2}{\sqrt{x} + 2} = \lim_{x \longrightarrow 4} \dfrac{\sqrt{x}^2 - 2^2}{(x-1)(x-4)} \times \dfrac{1}{\sqrt{x} + 2} = \lim_{x \longrightarrow 4} \dfrac{x - 4}{(x-1)(x-4)} \times \dfrac{1}{\sqrt{x} + 2}$$
Ce qui nous donne en simplifiant par $$(x-4)$$ :
$$\lim_{x \longrightarrow 4} \dfrac{\sqrt{x} - 2}{x^2 - 5x + 4} = \lim_{x \longrightarrow 4} \dfrac{1}{(x-1) \, (\sqrt{x} + 2)} = \dfrac{1}{(4-1) \, (\sqrt{4} + 2)} = \dfrac{1}{3 \, (2 + 2)} = \dfrac{1}{3 \times 4} = \dfrac{1}{12}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{d}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, définition \,\, du \,\, nombre \,\, dérivée \,\, en} \,\, x=1 }}$$
En effet, en utilisant la définition de la dérivée en $$1$$, on trouve que :
$$\lim_{x \longrightarrow 1} \dfrac{\sqrt[3]{x} - 1}{x-1} = \left( \sqrt[3]{x} \right)'(x=1) = \left( x^{\frac{1}{3}} \right)'(x=1) = \left( \dfrac{1}{3} x^{\frac{1}{3}-1} \right)(x=1) = \left( \dfrac{1}{3} x^{-\frac{2}{3}} \right)(x=1) = \dfrac{1}{3} \times 1^{-\frac{2}{3}} = \dfrac{1}{3} \times 1 = \dfrac{1}{3}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{d}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, méthode \,\, de \,\, factorisation \,\, par \,\, le \,\, terme \,\, de \,\, puissance \,\, la \,\, plus \,\, importante }}}$$
En factorisant par $$x^2$$ dans chacune des racines carrées présentent, on trouve que :
$$\lim_{x \longrightarrow 1} \dfrac{\sqrt{x^2 + x} - \sqrt{x^2 + 1}}{\sqrt{3x^2 + 2x} - \sqrt{3x^2 + x + 1}} = \lim_{x \longrightarrow 1} \dfrac{\sqrt{3 + \dfrac{2}{x}} + \sqrt{3 + \dfrac{1}{x} + \dfrac{1}{x^2}}}{\sqrt{1 + \dfrac{1}{x}} +\sqrt{1 + \dfrac{1}{x^2}}} = \dfrac{\sqrt{3 + \dfrac{2}{1}} + \sqrt{3 + \dfrac{1}{1} + \dfrac{1}{1^2}}}{\sqrt{1 + \dfrac{1}{1}} +\sqrt{1 + \dfrac{1}{1^2}}} = \dfrac{\sqrt{3 + 2} + \sqrt{3 + 1 + 1}}{\sqrt{1 + 1} +\sqrt{1 + 1}} = \dfrac{\sqrt{5}+\sqrt{5}} {\sqrt{2}+\sqrt{2}} = \dfrac{2\sqrt{5}}{2\sqrt{2}} = \dfrac{\sqrt{5}}{\sqrt{2}} = \sqrt{\dfrac{5}{2}}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{d}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, un \,\, jeu \,\, d'écriture \,\, et \,\, la \,\, définition \,\, du \,\, nombre \,\, dérivée \,\, en} \,\, x=a }}$$
En effet, on a :
$$\lim_{x \longrightarrow a} \dfrac{x^\alpha - a^\alpha}{x^\beta - a^\beta} = \lim_{x \longrightarrow a} \left( \dfrac{x^\alpha - a^\alpha}{x - a} \times \dfrac{x- a}{x^\beta - a^\beta} \right) = \lim_{x \longrightarrow a} \left( \dfrac{x^\alpha - a^\alpha}{x - a} \times \dfrac{1}{\dfrac{x^\beta - a^\beta}{x- a}} \right) = \lim_{x \longrightarrow a} \dfrac{x^\alpha - a^\alpha}{x - a} \times \dfrac{1}{\displaystyle{\lim_{x \longrightarrow a}} \dfrac{x^\beta - a^\beta}{x- a}}$$
On reconnait alors la définition de la dérivation en $$a$$, et on obtient alors :
$$\lim_{x \longrightarrow a} \dfrac{x^\alpha - a^\alpha}{x^\beta - a^\beta} = \dfrac{\left( x^\alpha \right)'(x=a)}{\left( x^\beta \right)'(x=a)} = \dfrac{\left( \alpha x^{\alpha-1} \right)(x=a)}{\left( \beta x^{\beta-1} \right)(x=a)} = \dfrac{\alpha a^{\alpha-1}}{\beta a^{\beta-1}} = \dfrac{\alpha}{\beta} \dfrac{a^{\alpha-1}}{a^{\beta-1}} = \dfrac{\alpha}{\beta} a^{\alpha-1 - (\beta-1)} = \dfrac{\alpha}{\beta} a^{\alpha-1 - \beta + 1} = \dfrac{\alpha}{\beta} a^{\alpha-\beta }$$

$$\red{\text{La bonne réponse est}}$$ $$\red{c}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, formule \,\, de \,\, dérivation \,\, suivante \,\, : } \,\, \left(\dfrac{1}{f}\right)' = \dfrac{-f'}{f^2} }}$$
En effet, soit $$x \in \left[ \dfrac{\pi}{4} \,;\ \dfrac{\pi}{3} \right]$$. L'expression $$f'$$ de la dérivée de $$f(x) = \dfrac{1}{\sin\left( \dfrac{1}{x} \right)}$$ est :
$$f'(x) = \dfrac{-\left( \sin\left( \dfrac{1}{x} \right) \right)'}{\sin^2\left( \dfrac{1}{x} \right)} = \dfrac{- \left( \dfrac{1}{x} \right)' \times \cos\left( \dfrac{1}{x} \right) }{\sin^2\left( \dfrac{1}{x} \right)} = \dfrac{- \dfrac{-1}{x^2} \times \cos\left( \dfrac{1}{x} \right) }{\sin^2\left( \dfrac{1}{x} \right)} = \dfrac{\cos\left( \dfrac{1}{x} \right) }{x^2 \sin^2\left( \dfrac{1}{x} \right)} = \dfrac{\cos^2\left( \dfrac{1}{x} \right) }{x^2 \cos\left( \dfrac{1}{x} \right) \sin^2\left( \dfrac{1}{x} \right)} = \dfrac{1}{x^2 \cos\left( \dfrac{1}{x} \right) \dfrac{ \sin^2\left( \dfrac{1}{x} \right)}{\cos^2\left( \dfrac{1}{x} \right) }} = \dfrac{1}{x^2 \cos\left( \dfrac{1}{x} \right) \tan^2\left( \dfrac{1}{x} \right)}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{c}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, formule \,\, de \,\, dérivation \,\, suivante \,\, : } \,\, \left(\ln(f)\right)' = \dfrac{f'}{f} }}$$
En effet, on a :
$$f'(x) = \left(\ln\left( \cos^2(\sqrt{x} + 1) \right)\right)' = \dfrac{\left( \cos^2(\sqrt{x} + 1) \right)'}{\cos^2(\sqrt{x} + 1)} = \dfrac{2 \cos(\sqrt{x} + 1) \left( \cos(\sqrt{x} + 1) \right)'}{\cos^2(\sqrt{x} + 1)} = \dfrac{2 \cos(\sqrt{x} + 1) \times (\sqrt{x} + 1)' \times -\sin(\sqrt{x} + 1) }{\cos^2(\sqrt{x} + 1)}$$
Ce qui nous donne :
$$f'(x) = \dfrac{2 \cos(\sqrt{x} + 1) \times \dfrac{1}{2\sqrt{x}} \times -\sin(\sqrt{x} + 1) }{\cos^2(\sqrt{x} + 1)} = - \dfrac{ \dfrac{1}{\sqrt{x}} \sin(\sqrt{x} + 1) }{\cos(\sqrt{x} + 1)} = -\dfrac{\tan(\sqrt{x} + 1 )}{\sqrt{x}}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{a}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, formule \,\, de \,\, dérivation \,\, suivante \,\, : } \,\, \left(f^2\right)' = 2 f'f }}$$
En effet, on a :
$$f'(x) = \left( \cos^2\left( \ln \left(\sqrt{x} + 1 \right) \right) \right)'= 2 \cos\left( \ln \left(\sqrt{x} + 1 \right) \right) \left( \cos\left( \ln \left(\sqrt{x} + 1 \right) \right) \right)' = 2 \cos\left( \ln \left(\sqrt{x} + 1 \right) \right) \left( \ln \left(\sqrt{x} + 1 \right) \right)' \times -\sin\left( \ln \left(\sqrt{x} + 1 \right) \right)$$
Mais $$\left( \ln \left(\sqrt{x} + 1 \right) \right)' = \dfrac{(\sqrt{x} + 1 )'}{\sqrt{x} + 1 } = \dfrac{ \dfrac{1}{2\sqrt{x}} }{\sqrt{x} + 1 } = \dfrac{1}{2\sqrt{x} \left( \sqrt{x} + 1 \right)}$$. Ainsi, on obtient :
$$f'(x) = - 2 \cos\left( \ln \left(\sqrt{x} + 1 \right) \right) \dfrac{1}{2\sqrt{x} \left( \sqrt{x} + 1 \right)} \sin\left( \ln \left(\sqrt{x} + 1 \right) \right) = - \dfrac{2 \cos\left( \ln \left(\sqrt{x} + 1 \right) \right) \sin\left( \ln \left(\sqrt{x} + 1 \right) \right) }{2\sqrt{x} \left( \sqrt{x} + 1 \right)}$$
Mais pour tout $$X$$ réel, on sait que $$2 \cos(X) \sin(X) = \sin(2X)$$. Finalement, on trouve que :
$$f'(x) = - \dfrac{\sin\left( 2\ln \left(\sqrt{x} + 1 \right) \right) }{2\sqrt{x} \left( \sqrt{x} + 1 \right)}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{b}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, formule \,\, de \,\, dérivation \,\, suivante \,\, : } \,\, \left(\ln(f)\right)' = \dfrac{f'}{f} }}$$
En effet, pour $$x \geqslant 2$$, on a :
$$f'(x) = \left( \ln \left( \ln \left( \ln \left( x^2\right) \right) \right) \right)'= \dfrac{\left( \ln \left( \ln \left( x^2\right) \right) \right)'}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\left( \ln \left( x^2\right) \right)'}{\ln \left( x^2\right)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\dfrac{(x^2)'}{x^2}}{\ln \left( x^2\right)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\dfrac{2x}{x^2}}{\ln \left( x^2\right)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\dfrac{2}{x}}{\ln \left( x^2\right)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\dfrac{2}{x}}{2\ln(x)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{\dfrac{1}{x}}{\ln(x)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{\dfrac{1}{x\ln(x)}}{\ln \left( \ln \left( x^2\right) \right)} = \dfrac{1}{x\ln(x)\ln \left( \ln \left( x^2\right) \right)}$$
Mais comme $$\ln(x^2) = 2 \ln(x)$$, on a :
$$f'(x) = \dfrac{1}{x \ln(x) \ln \left( 2 \ln(x)\right)}$$

$$\red{\text{La bonne réponse est}}$$ $$\red{a}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, utiliser \,\, la \,\, définition \,\, du \,\, taux \,\, de \,\, variation \,\, (dérivée) \,\, en} \,\, x=0^+ \,\, \mathrm{et \,\, en \,\,} x=0^- }}$$
En effet, on a :
$$\lim_{x \longrightarrow 0^\pm} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \longrightarrow 0^\pm} \dfrac{|\, \sin(x)\,| - |\, \sin(0)\,|}{x} = \lim_{x \longrightarrow 0^\pm} \dfrac{|\, \sin(x)\,| - |\, 0 \,|}{x} = \lim_{x \longrightarrow 0^\pm} \dfrac{|\, \sin(x)\,|}{x}$$
Or, lorsque $$x$$ tend vers $$0$$, le terme $$\sin(x)$$ est équivalent à $$x$$. Ce qui nous permet d'écrire que :
$$\lim_{x \longrightarrow 0^\pm} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \longrightarrow 0^\pm} \dfrac{|\, x \,|}{x}$$
$$\,\, \bullet \,\,$$ si $$x \longrightarrow 0^+$$ alors $$x>0$$ et $$|\, x \,| = x$$
Dans ce cas, on a :
$$\lim_{x \longrightarrow 0^+} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \longrightarrow 0^+} \dfrac{x}{x} = \lim_{x \longrightarrow 0^+} 1 = 1$$
$$\,\, \bullet \bullet \,\,$$ si $$x \longrightarrow 0^-$$ alors $$x<0$$ et $$|\, x \,| = -x$$
Dans ce cas, on a :
$$\lim_{x \longrightarrow 0^-} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \longrightarrow 0^-} \dfrac{-x}{x} = \lim_{x \longrightarrow 0^-} -1 = -1$$
On constate alors que :
$$\lim_{x \longrightarrow 0^+} \dfrac{f(x) - f(0)}{x - 0} \neq \lim_{x \longrightarrow 0^-} \dfrac{f(x) - f(0)}{x - 0}$$
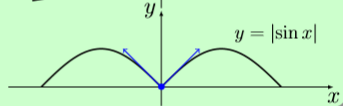
Donc la fonction $$f$$ n'est pas dérivable à l'origine. Il y a l'existence de deux tangentes différentes au point origine.
Graphiquement, ceci se visualise très bien :

$$\red{\text{La bonne réponse est}}$$ $$\red{c}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, penser \,\, à \,\, la \,\, formule \,\, suivante \,\, : } \,\, \left(\ln(f)\right)' = \dfrac{f'}{f} }}$$
En effet, on a :
$$\int_{0}^{\frac{\pi}{3}} \dfrac{\sin(x)}{2 - \cos(x)} \, dx = \int_{0}^{\frac{\pi}{3}} \dfrac{\left( 2 - \cos(x) \right)'}{2 - \cos(x)} \, dx = [\ln\left( 2 - \cos(x) \right)]_{0}^{\frac{\pi}{3}} = \ln\left( 2 - \cos\left( \dfrac{\pi}{3} \right) \right) - \ln\left( 2 - \cos\left( 0 \right) \right) = \ln\left( 2 - \dfrac{1}{2} \right) - \ln\left( 2 - 1 \right) = \ln\left( \dfrac{3}{2} \right) - \ln\left( 1 \right) = \ln\left( \dfrac{3}{2} \right) - 0 = \ln\left( \dfrac{3}{2} \right)$$

$$\red{\text{La bonne réponse est}}$$ $$\red{b}$$
$$\red{\boxed{\mathrm{Il \,\,faut \,\, penser \,\, à \,\, une \,\, décomposition \,\, simple \,\, et \,\, aux \,\, deux \,\, formules \,\, suivantes \,\, : } \,\, \left( f^2 \right)'= 2f'f \,\, \mathrm{et} \,\, \left(\tan(x)\right)' = \dfrac{1}{\cos^2(x)} }}$$
En effet, on a :
$$\int_{0}^{\frac{\pi}{4}} \dfrac{1+\tan(x)}{\cos^2(x)} \, dx = \int_{0}^{\frac{\pi}{4}} \left( \dfrac{1}{\cos^2(x)} + \dfrac{\tan(x)}{\cos^2(x)} \right) \, dx = \int_{0}^{\frac{\pi}{4}} \dfrac{1}{\cos^2(x)} \, dx + \int_{0}^{\frac{\pi}{4}} \dfrac{1}{\cos^2(x)} \tan(x) \, dx = \int_{0}^{\frac{\pi}{4}} \dfrac{1}{\cos^2(x)} \, dx + \dfrac{1}{2}\int_{0}^{\frac{\pi}{4}} 2\dfrac{1}{\cos^2(x)} \tan(x) \, dx$$
Or le terme $$\dfrac{1}{\cos^2(x)}$$ est la dérivée de $$\tan(x)$$. Ainsi, on obtient :
$$\int_{0}^{\frac{\pi}{4}} \dfrac{1+\tan(x)}{\cos^2(x)} \, dx = [\tan(x)]_{0}^{\frac{\pi}{4}} + \dfrac{1}{2} [\tan^2(x)]_{0}^{\frac{\pi}{4}} = \tan\left( \dfrac{\pi}{4} \right) - \tan(0) + \dfrac{\tan^2\left( \dfrac{\pi}{4} \right) - \tan^2(0)}{2} = 1 - 0 + \dfrac{1 - 0}{2} = \dfrac{3}{2}$$