Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Pour bien poursuivre - Exercice 1
30 min
45
Calculer les intégrales suivantes :
Question 1
Correction
On a :
Soit encore :
Or, si on pose alors . Dans ce cas, on constate que . Ceci s'intègre directement en avec . On a alors :
Ce qui nous donne, en faisant usage des propriétés des logarithmes :
Finalement, on obtient :
Soit encore :
Or, si on pose alors . Dans ce cas, on constate que . Ceci s'intègre directement en avec . On a alors :
Ce qui nous donne, en faisant usage des propriétés des logarithmes :
Finalement, on obtient :
Question 2
Correction
On a :
Si on pose alors . Dans ce cas, on obtient la forme suivante :
En utilisant les propriétés algébriques usuelles associées aux logarithmes, on obtient :
Finalement :
Si on pose alors . Dans ce cas, on obtient la forme suivante :
En utilisant les propriétés algébriques usuelles associées aux logarithmes, on obtient :
Finalement :
Question 3
Correction
Soit une quantité réelle. On sait que . Mais également que . On a alors :
On pose ce qui implique que . Ainsi une forme apparait, et s'intègre aisément en . Nous poserons dans la suite, ce qui ne change rien pour l'évaluation d'une intégrale. Ce qui nous donne donc :
Soit encore :
Finalement, on obtient :
On pose ce qui implique que . Ainsi une forme apparait, et s'intègre aisément en . Nous poserons dans la suite, ce qui ne change rien pour l'évaluation d'une intégrale. Ce qui nous donne donc :
Soit encore :
Finalement, on obtient :
Question 4
Correction
Posons . Cette fonction admet une valeur interdite en , elle y est donc discontinue.
D'autre part, on a les deux limites suivantes :
et
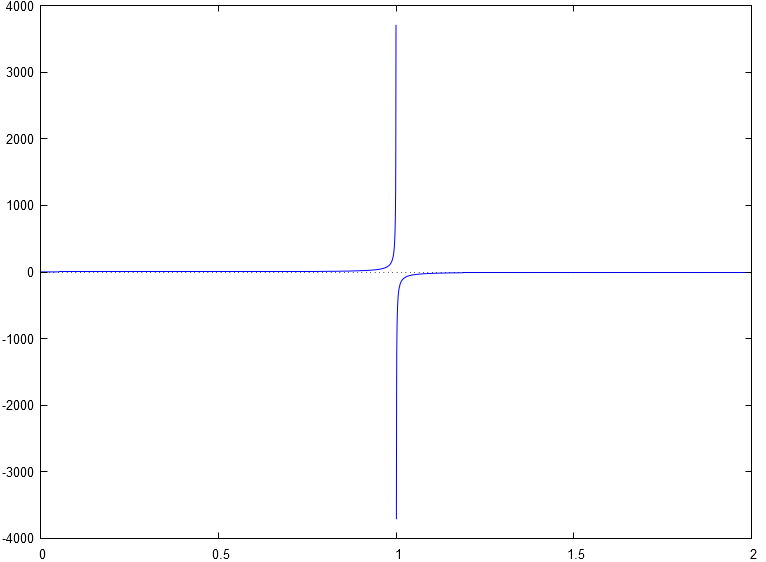
Ainsi l'intégrale , qui représente l'aire algébrique associée à sur l'intervalle , prend une valeur infinie, et non une valeur finie réelle. On dit qu'elle diverge.
Graphiquement, on observe parfaitement bien cela :
D'autre part, on a les deux limites suivantes :
et
Ainsi l'intégrale , qui représente l'aire algébrique associée à sur l'intervalle , prend une valeur infinie, et non une valeur finie réelle. On dit qu'elle diverge.
Graphiquement, on observe parfaitement bien cela :
