Vers la prépa (3) - Exercice 1

L'équa
tion étant linéaire, la solution générale $$y$$ sera la somme de : ;
$$\,\, \bullet \,\,$$ la solution homogène (ou sans second membre) de l'équation sans second membre. On la notera $$y_{ssm}$$ ;
$$\,\, \bullet \,\,$$ la solution particulière (ou sans second membre) de l'équation globale. On la notera $$y_{p}$$.
$$\,\,\,\,\,\,\,\,\, \clubsuit \,\,$$ Recherche de a solution sans second membre, ou homogène.
On considère l'équation sans second membre $$(E_1)$$ suivante :
$$(E_1) : \,\, x\, y_{ssm}' - y_{ssm} = 0$$
On a alors :
$$x\, y'_{ssm} = y_{ssm} \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{y'_{ssm}}{y_{ssm}} = \dfrac{1}{x}$$
En primitivant, on trouve que :
$$\ln(y_{ssm}(x)) = \ln(x) + k \,\, (k \in \mathbb{R})$$
Ainsi, on trouve que :
$$y_{ssm}(x) = e^{\ln(x) + k} \,\,\,\, \Longleftrightarrow \,\,\,\, y_{ssm}(x) = e^{\ln(x)} \times e^k\,\,\,\, \Longleftrightarrow \,\,\,\, y_{ssm}(x) = x \times e^k$$
En posant $$C = e^k$$, avec $$C\in \mathbb{R}$$, on obtient :
$$y_{ssm}(x) = C \, x$$
$$\,\,\,\,\,\,\,\,\, \clubsuit \,\,$$ Recherche de a solution particulière.
$$x\, y_p' - y_p = x^3 + 1$$
Le second membre étant un polynôme du troisième degré, nous allons donc choisir une solution particulière de la même nature. C'est pourquoi, avec les quatre nombres réels $$a$$, $$b$$, $$c$$ et $$d$$, on pose :
$$y_p(x) = ax^3 + bx^2 + cx + d \,\,\,\, \Longrightarrow \,\,\,\, y_p(x) = 3ax^2 + 2bx + c$$
Ainsi :
$$x\, (3ax^2 + 2bx + c) - (ax^3 + bx^2 + cx + d) = x^3 + 1 \,\,\,\, \Longleftrightarrow \,\,\,\, 3ax^3 + 2bx^2 + cx - ax^3 - bx^2 - cx - d = x^3 + 1$$
En simplifiant :
$$2ax^3 + bx^2 - d = x^3 + 1$$
En regroupant les terme de même nature :
Soit :
$$2ax^3 - x^3 + bx^2 - d - 1 = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, (2a-1)x^3 + bx^2 - (d + 1) = 0$$
Ce qui implique que :
$$a = \dfrac{1}{2} \,\,\, ; \,\,\, b = 0 \,\,\, ; \,\,\, d = -1$$
On a alors :
$$y_p(x) = \dfrac{1}{2}x^3 + cx - 1$$
$$\,\,\,\,\,\,\,\,\, \clubsuit \,\,$$ Recherche de a solution globale.
Comme l'équation différentielle $$(E)$$ est linéaire, cela nous permet de dire que :
$$y(x) = y_{ssm}(x) + y_p(x)$$
Donc :
$$y(x) = Cx + \dfrac{1}{2}x^3 + cx - 1$$
Ce qui nous permet d'écrire :
$$y(x) = (C+c)x + \dfrac{1}{2}x^3 - 1$$
On pose alors $$K = (C + c) \in \mathbb{R}$$, on a alors la solution générale suivante :
$$y(x) = \dfrac{1}{2}x^3 + Kx - 1$$
Parmi toutes les solutions précédentes, une seule d'entre-elles satisfait à la condition $$y(x = 1) = 0$$. On a alors :
$$y(x = 1) = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{1}{2} \times 1^3 + K\times 1 - 1 = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{1}{2} + K - 1 = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, K = 1 - \dfrac{1}{2} \,\,\,\, \Longleftrightarrow \,\,\,\, K = \dfrac{1}{2}$$
Ce qui nous permet d'écrire que :
$$y(x) = \dfrac{1}{2}x^3 + \dfrac{1}{2}x - 1$$
Soit encore :
$$y(x) = \dfrac{x^3 + x - 2}{2}$$
Le polynôme $$x^3 + x - 2$$ admet comme racine évidente $$1$$. Ainsi, il est possible de factoriser $$x^3 + x - 2$$ par $$x-1$$. On a alors :
$$x^3 + x - 2 = (x - 1) (x^2 + x +2)$$
Finalement, on trouve que :
$${\color{red}{\boxed{y(x) = \dfrac{(x - 1) (x^2 + x +2)}{2}}}}$$
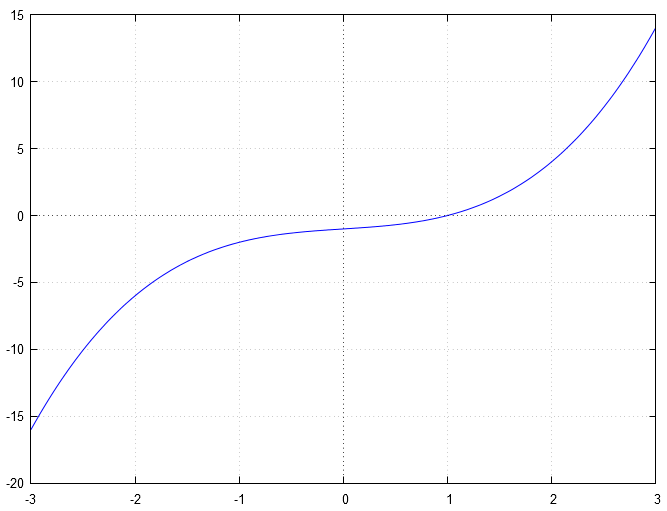
Ce qui nous donne graphiquement :