Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Etude d'une fonction numérique - Exercice 1
1 h
90
Soit la fonction numérique, de la variable réelle , définit par :
Pour ,
Pour ,
Pour ,
Pour ,
Question 1
Etudier la continuité de sur .
Correction
La fonction exponentielle exponentielle est continue sur . Puis, la fonction inverse au carré est continue sur . Donc, le produit des deux est continue sur . Ceci traduit que la division par zéro n'a pas de sens. En effet, partager par rien est dénué de sens. Ainsi la fonction est continue sur .
La continuité en requiert une attention particulière par l'étude des limites lorsque et .
La continuité en requiert une attention particulière par l'étude des limites lorsque et .
Question 2
Etudier la continuité de en . Vous distinguerez les cas et .
Correction
Si la fonction soit être continue en alors on aura les égalités suivantes :
Si l'une de ces égalités n'est pas vérifiée alors la fonction ne sera pas continue en .
On a :
limite lorsque
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Donc :
Ainsi, l'axe des ordonnées est une asymptote verticale à la courbe représentative de lorsque .
limite lorsque
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Le théorème des croissances comparées, en , nous apprend que le exponentiel à une vitesse de décroissance beaucoup plus importante que la croissance polynomiale du terme . Donc, on en déduit que :
Et de fait :
CONCLUSION :
On vient de montrer que , ce qui implique que la fonction n'est pas continue en .
Si l'une de ces égalités n'est pas vérifiée alors la fonction ne sera pas continue en .
On a :
limite lorsque
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Donc :
Ainsi, l'axe des ordonnées est une asymptote verticale à la courbe représentative de lorsque .
limite lorsque
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Le théorème des croissances comparées, en , nous apprend que le exponentiel à une vitesse de décroissance beaucoup plus importante que la croissance polynomiale du terme . Donc, on en déduit que :
Et de fait :
CONCLUSION :
On vient de montrer que , ce qui implique que la fonction n'est pas continue en .
Question 3
Etudier la dérivabilité de en . Vous distinguerez les cas et .
Correction
Etudions la dérivabilité de en
D'après la question précédente, l'axe des ordonnées est une asymptote verticale. Ceci signifie que, lorsque , le coefficient de la tangente tend vers . Ainsi, la fonction n'est pas dérivable lorsque . On dit encore que n'est pas dérivable à "gauche" de l'origine.
Etudions la dérivabilité de en
On cherche la dérivabilité de , à "droite" de on on note cela par . On a, par définition, la limite suivante :
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Le théorème des croissances comparées, en , nous apprend que le exponentiel à une vitesse de décroissance beaucoup plus importante que la croissance polynomiale du terme . Donc, on en déduit que :
Et de fait :
Ainsi la fonction est dérivable en . La tangente à l'origine est horizontale et tournée vers la droite.
D'après la question précédente, l'axe des ordonnées est une asymptote verticale. Ceci signifie que, lorsque , le coefficient de la tangente tend vers . Ainsi, la fonction n'est pas dérivable lorsque . On dit encore que n'est pas dérivable à "gauche" de l'origine.
Etudions la dérivabilité de en
On cherche la dérivabilité de , à "droite" de on on note cela par . On a, par définition, la limite suivante :
On pose , ainsi . De fait, on en déduit que si alors . Ainsi, on peut écrire que :
On a alors :
Le théorème des croissances comparées, en , nous apprend que le exponentiel à une vitesse de décroissance beaucoup plus importante que la croissance polynomiale du terme . Donc, on en déduit que :
Et de fait :
Ainsi la fonction est dérivable en . La tangente à l'origine est horizontale et tournée vers la droite.
Question 4
Etudiez les variations de sur
Correction
La fonction étudiée est donc dérivable sur l'intervalle . Et la fonction dérivée associée est donnée par :
Or, sur l'intervalle , le terme est toujours strictement positif, puis le terme est également strictement positif. Ainsi, sur l'intervalle , la dérivée est du même signe que le terme (polynomial de premier degré) . On peut donc écrire que :
pour , on a , ce qui implique que .
pour , on a , ce qui implique que .
pour , on a , ce qui implique que .
On constate qu'en , la dérivée s'annule en changeant de signe, passant de la positivité à la négativité. Donc en , la courbe représentative de la fonction admet un maximum local. Le principe de Lagrange permet alors de conclure sur les variations de , à savoir :
pour , est croissante, et admet une discontinuité à l'origine, donc en .
pour , présente un maximum local de valeur .
pour , est décroissante.
Avec :
Il nous reste à étudier les limites de en ainsi qu'en . Lorsque , on a , et de fait . Il s'ensuit que :
Cependant, on a . Ainsi, on en déduit aisément que :
Donc, lorsque , l'axe des abscisses est une asymptote à la courbe représentative de la fonction .
Or, sur l'intervalle , le terme est toujours strictement positif, puis le terme est également strictement positif. Ainsi, sur l'intervalle , la dérivée est du même signe que le terme (polynomial de premier degré) . On peut donc écrire que :
pour , on a , ce qui implique que .
pour , on a , ce qui implique que .
pour , on a , ce qui implique que .
On constate qu'en , la dérivée s'annule en changeant de signe, passant de la positivité à la négativité. Donc en , la courbe représentative de la fonction admet un maximum local. Le principe de Lagrange permet alors de conclure sur les variations de , à savoir :
pour , est croissante, et admet une discontinuité à l'origine, donc en .
pour , présente un maximum local de valeur .
pour , est décroissante.
Avec :
Il nous reste à étudier les limites de en ainsi qu'en . Lorsque , on a , et de fait . Il s'ensuit que :
Cependant, on a . Ainsi, on en déduit aisément que :
Donc, lorsque , l'axe des abscisses est une asymptote à la courbe représentative de la fonction .
Question 5
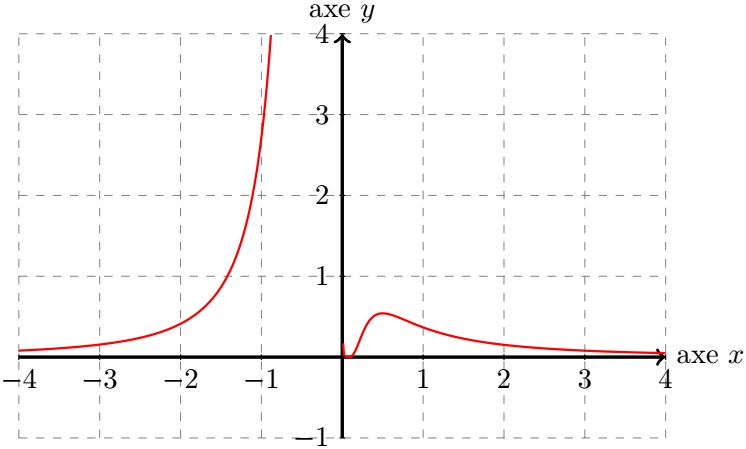
Construire la courbe représentative de .
Correction
On a le graphique suivant :