Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 1 - Premiers pas - Exercice 1
45 min
60
La trigonométrie est omniprésente en Sciences. Son étude et sa maîtrise sont essentielles pour se sentir en confiance dans son usage au travers de différentes disciplines mais également au seins des différentes branches de ces disciplines. En Physique, la trigonométrie est présente en Mécanique, Mécanique des fluides, Astronautique, Electromagnétisme, Electronique, Electrocinétique, Thermodynamique, Géophysique ...
Bref, ne pas maîtriser les techniques élémentaires peut rapidement se révéler être particulièrement pénalisant !
Bref, ne pas maîtriser les techniques élémentaires peut rapidement se révéler être particulièrement pénalisant !
Question 1
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Positionnons cela sur un cercle trigonométrique en ayant en tête que et sont des angles associés.
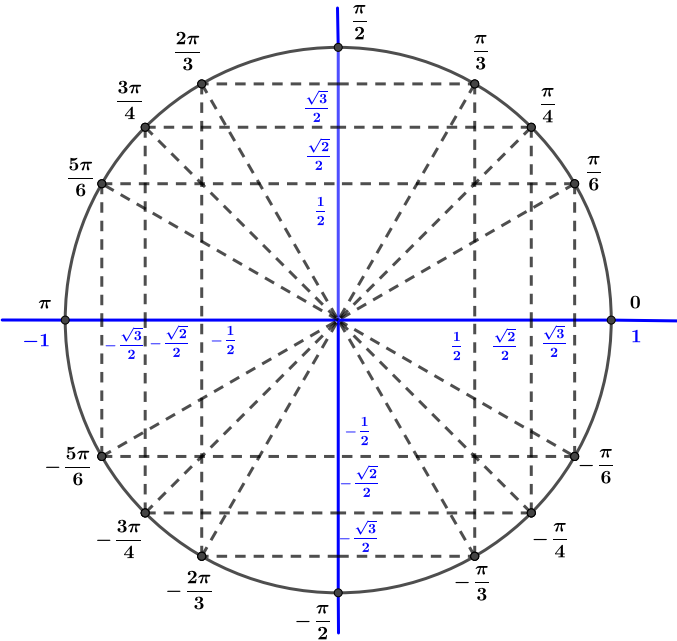
On remarque alors que :
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Positionnons cela sur un cercle trigonométrique en ayant en tête que et sont des angles associés.

On remarque alors que :
Finalement, l'ensemble des solutions de l'équation sont :
Question 2
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :
Question 3
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Finalement, l'ensemble des solutions de l'équation sont :
Question 4
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Soit, en divisant par , on obtient :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Soit, en divisant par , on obtient :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :
Question 5
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Donc, on en déduit que :
Ceci nous permet d'écrire que :
Or :
Cette dernière inégalité est strictement impossible puisque le cosinus est borné entre et . L'équation n'as donc pas de solution sur .
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Donc, on en déduit que :
Ceci nous permet d'écrire que :
Or :
Cette dernière inégalité est strictement impossible puisque le cosinus est borné entre et . L'équation n'as donc pas de solution sur .
Finalement, l'ensemble des solutions de l'équation sont :
Question 6
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
Soit :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ainsi, on en déduit que :
On a alors :
On écrit alors que :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Finalement, l'ensemble des solutions de l'équation sont :
Soit :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ainsi, on en déduit que :
On a alors :
On écrit alors que :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Finalement, l'ensemble des solutions de l'équation sont :
Question 7
Résoudre, dans , l'équation suivante : .
Correction
En appliquant la méthode décrite précédemment, avec , on a :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ainsi :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Soit, en divisant par , on obtient :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :
On recherche donc un nombre réel qui vérifient les deux conditions :
Ainsi :
Ceci nous permet d'écrire que :
Ce qui s'écrit encore :
Ainsi, avec , on a :
Soit, en divisant par , on obtient :
Il n'est pas possible de compacter cette écriture des solutions recherchées.
Finalement, l'ensemble des solutions de l'équation sont :