Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Variation d'une fonction intégrale - Exercice 1
30 min
50
Plus original ...
Question 1
Soit . Soit la fonction suivante :
Etudier la parité de .
Correction
La fonction est définie (donc continue) sur , de fait également.
On a alors, , le résultat suivant :
Posons dans ce cas et lorsque va de à on constate que va de à , donc :
Donc la fonction est impaire.
On a alors, , le résultat suivant :
Posons dans ce cas et lorsque va de à on constate que va de à , donc :
Donc la fonction est impaire.
Question 2
Etudier, sur , les variations de .
Correction
Nous allons étudier les variations de sur , puis par imparité, deviner celles sur , donc sur tout entier.
Donc , donc .
La fonction est strictement positive sur , et de fait la fonction est strictement positive si et nulle si (car les deux bornes de l'intégrale seraient alors les mêmes).
Soit tel que . On a alors l'écriture suivante :
Ceci peut également s'écrire comme :
Et de fait :
Donc, on en déduit immédiatement que :
Soit encore :
Ce qui nous donne :
On constate que .
Supposons maintenant que . Dans ce cas, on a alors :
Donc :
Ce qui implique, en élevant au carré, que :
D'où :
Comme , on a donc uniquement :
Donc :
Ce qui nous permet d'affirmer que la fonction est croissante lorsque .
Puis, on constate que :
Et comme , on a donc uniquement :
Ce qui signifie que correspond à un maximum de sur , et ce maximum représente l'aire sous la courbe représentative de la fonction positive entre les abscisses et . Graphiquement, cela correspond à la situation suivante :
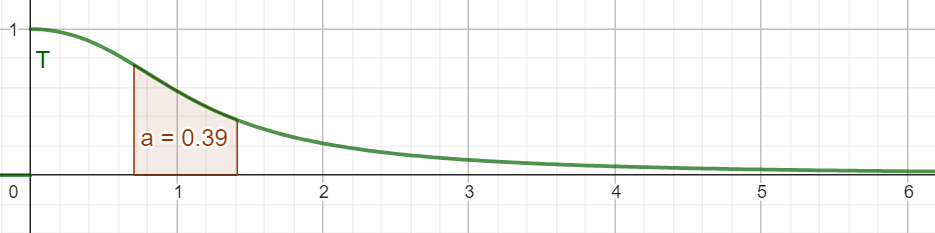
Notons par ce maximum, et ce dernier vaut (numériquement) environ .
Donc, on en déduit que lorsque la fonction est décroissante. Mais nous n'avons à ce stade pas de renseignement sur la limite de lorsque . En effet, nous savons "simplement" que est strictement positive si . C'est pourquoi nous allons déterminer la limite de lorsque . On a alors :
Donc, on en déduit que :
Comme , cela implique que :
Avec :
Par passage à la limite, on a :
Soit :
Or . Donc le théorème de l'encadrement nous permet de conclure que :
Ce qui revient à dire que :
.
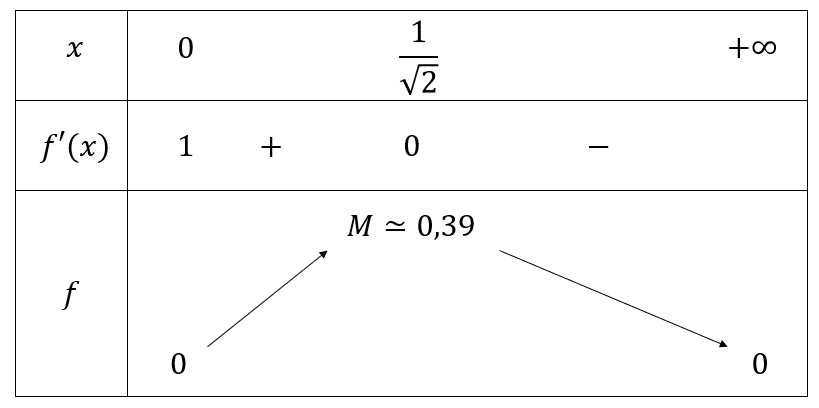
Donc, on a le tableau de variation de sur suivant :
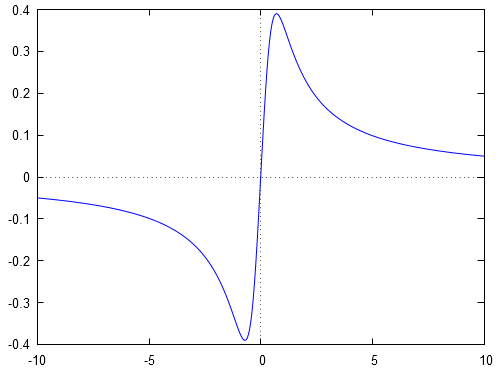
Ceci se vérifie bien graphiquement. En effet, à l'aide d'un logiciel de calcul numérique, on trouve que la courbe représentative de la fonction est :
Donc , donc .
La fonction est strictement positive sur , et de fait la fonction est strictement positive si et nulle si (car les deux bornes de l'intégrale seraient alors les mêmes).
Soit tel que . On a alors l'écriture suivante :
Ceci peut également s'écrire comme :
Et de fait :
Donc, on en déduit immédiatement que :
Soit encore :
Ce qui nous donne :
On constate que .
Supposons maintenant que . Dans ce cas, on a alors :
Donc :
Ce qui implique, en élevant au carré, que :
D'où :
Comme , on a donc uniquement :
Donc :
Ce qui nous permet d'affirmer que la fonction est croissante lorsque .
Puis, on constate que :
Et comme , on a donc uniquement :
Ce qui signifie que correspond à un maximum de sur , et ce maximum représente l'aire sous la courbe représentative de la fonction positive entre les abscisses et . Graphiquement, cela correspond à la situation suivante :

Notons par ce maximum, et ce dernier vaut (numériquement) environ .
Donc, on en déduit que lorsque la fonction est décroissante. Mais nous n'avons à ce stade pas de renseignement sur la limite de lorsque . En effet, nous savons "simplement" que est strictement positive si . C'est pourquoi nous allons déterminer la limite de lorsque . On a alors :
Donc, on en déduit que :
Comme , cela implique que :
Avec :
Par passage à la limite, on a :
Soit :
Or . Donc le théorème de l'encadrement nous permet de conclure que :
Ce qui revient à dire que :
.
Donc, on a le tableau de variation de sur suivant :

Ceci se vérifie bien graphiquement. En effet, à l'aide d'un logiciel de calcul numérique, on trouve que la courbe représentative de la fonction est :
