Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
On monte d'un niveau pour ces calculs de primitives - Exercice 1
1 h 40 min
140
Nous allons illustrer ces méthodes de calculs de primitives sur des premiers exemples. Il faut savoir être patient et prendre la précaution de vérifier les hypothèses et de poser l'ensemble de TOUS les calculs.
Question 1
Soit un nombre entier naturel non nul. On pose :
Déterminer une relation de récurrence entre les deux primitives et .
Puis, déterminer l'expression de .
Déterminer une relation de récurrence entre les deux primitives et .
Puis, déterminer l'expression de .
Correction
Nous allons commencer par déterminer une relation de récurrence entre les deux primitives et .
Pour cela, il semble que l'usage d'une intégration par parties s'impose. Pour cela écrivons :
On va intégrer et cela va donner et nous allons dériver le terme et nous avons :
Soit :
Donc, on obtient :
Soit :
Mais, on a :
Soit encore :
Ce qui nous donne donc :
D'où :
Ce qui s'écrit aussi :
Soit la relation de récurrence suivante :
Si on pose alors on trouve que :
Soit :
Or, on sait que :
Finalement, on en déduit que :
Pour cela, il semble que l'usage d'une intégration par parties s'impose. Pour cela écrivons :
On va intégrer et cela va donner et nous allons dériver le terme et nous avons :
Soit :
Donc, on obtient :
Soit :
Mais, on a :
Soit encore :
Ce qui nous donne donc :
D'où :
Ce qui s'écrit aussi :
Soit la relation de récurrence suivante :
Si on pose alors on trouve que :
Soit :
Or, on sait que :
Finalement, on en déduit que :
Question 2
Déterminer, sur , l'expression des primitives de la fonction suivante :
. Puis en déduire la valeur de .
. Puis en déduire la valeur de .
Correction
Posons . Donc . De fait . Ainsi, on en déduit que . En regroupant les termes en on trouve que : . En factorisant : . Finalement, on trouve que :
Ainsi, par dérivation de par rapport à , on a :
Donc :
D'où :
On a alors :
Ce qui s'écrit encore comme :
A l'aide d'une intégration par parties, on obtient :
Soit :
Soit encore :
La décomposition en éléments simples de l'expression nous donne :
Ainsi :
Ce qui nous donne donc :
Également :
On en déduit donc que :
En regroupant les termes :
Soit encore :
D'où :
On trouve donc que :
Or, . Donc . De fait :
Puis :
Ce qui, finalement, nous permet d'écrire que :
On peut alors écrire que :
Soit :
Et :
Soit, puisque :
Soit encore :
Donc :
D'où :
Ce qui nous donne :
On a alors :
Finalement :
On vérifie ceci numériquement (à l'aide d'un logiciel de calculs formels ou une calculatrice), et on obtient par exemple :
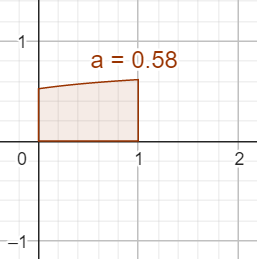
Ainsi, par dérivation de par rapport à , on a :
Donc :
D'où :
On a alors :
Ce qui s'écrit encore comme :
A l'aide d'une intégration par parties, on obtient :
Soit :
Soit encore :
La décomposition en éléments simples de l'expression nous donne :
Ainsi :
Ce qui nous donne donc :
Également :
On en déduit donc que :
En regroupant les termes :
Soit encore :
D'où :
On trouve donc que :
Or, . Donc . De fait :
Puis :
Ce qui, finalement, nous permet d'écrire que :
On peut alors écrire que :
Soit :
Et :
Soit, puisque :
Soit encore :
Donc :
D'où :
Ce qui nous donne :
On a alors :
Finalement :
On vérifie ceci numériquement (à l'aide d'un logiciel de calculs formels ou une calculatrice), et on obtient par exemple :

Question 3
Soit un nombre réel. On pose .
Déterminer la valeur de .
On donne, pour information, une partie du graphe de :
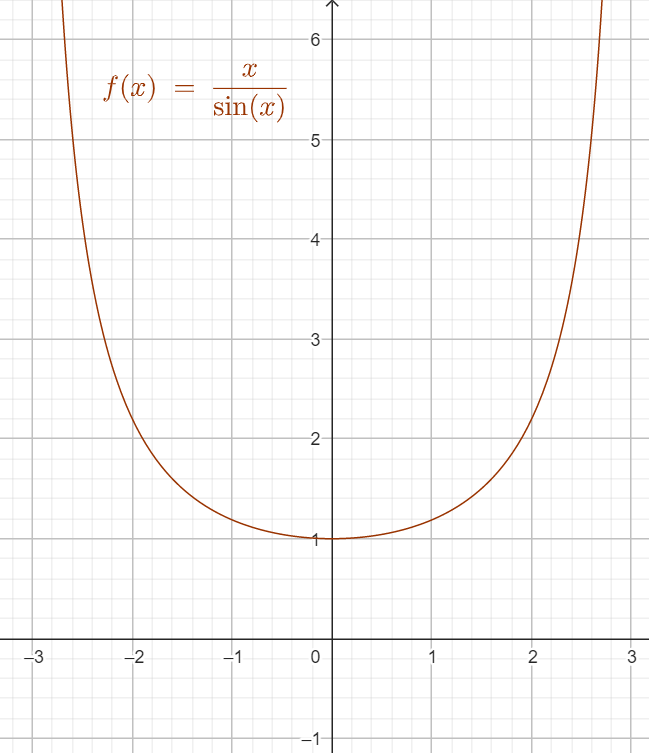
Déterminer la valeur de .
On donne, pour information, une partie du graphe de :

Correction
On constate que dur l'intervalle d'intégration considéré la fonction est continue et strictement croissante, donc réalise une bijection.
On va effectuer le changerment de variable "passe par tout" de la trigonométrie classique, à savoir, on pose . Donc, on en déduit que , et de fait :
Soit :
Puis :
Soit :
De plus, lorsque alors . Puis, lorsque alors . De fait, on obtient alors :
Soit :
Il faut maintenant faire usage de la technique de l'intégration par parties. Pour cela, on va intégrer le terme \dfrac{1}{u} pour obtenir , puis dériver le terme pour obtenir . On a alors :
Soit :
Notons . Effectuons le changement de variable (inspiré par les bornes). On en déduit que :
Donc :
Puis lorsque on a et si alors . De sorte que nous ayons :
Ce qui nous donne :
Donc ce qui implique que . Donc, on obtient :
Soit encore :
Ce qui nous donne :
Comme , on trouve que :
Ainsi :
En simplifiant, on trouve que :
Finalement :
On vérifie ceci numériquement (à l'aide d'un logiciel de calculs formels ou une calculatrice), et on obtient par exemple :
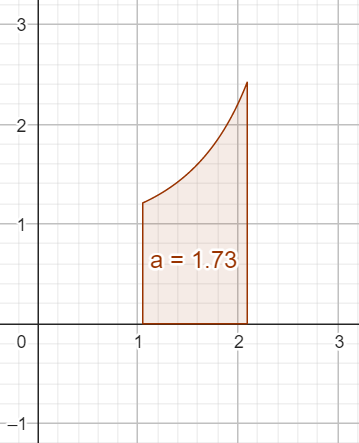
On va effectuer le changerment de variable "passe par tout" de la trigonométrie classique, à savoir, on pose . Donc, on en déduit que , et de fait :
Soit :
Puis :
Soit :
De plus, lorsque alors . Puis, lorsque alors . De fait, on obtient alors :
Soit :
Il faut maintenant faire usage de la technique de l'intégration par parties. Pour cela, on va intégrer le terme \dfrac{1}{u} pour obtenir , puis dériver le terme pour obtenir . On a alors :
Soit :
Notons . Effectuons le changement de variable (inspiré par les bornes). On en déduit que :
Donc :
Puis lorsque on a et si alors . De sorte que nous ayons :
Ce qui nous donne :
Donc ce qui implique que . Donc, on obtient :
Soit encore :
Ce qui nous donne :
Comme , on trouve que :
Ainsi :
En simplifiant, on trouve que :
Finalement :
On vérifie ceci numériquement (à l'aide d'un logiciel de calculs formels ou une calculatrice), et on obtient par exemple :

Question 4
Déterminer les primitives de .
Correction
On a :
D'où :
Donc :
Ce qui nous donne :
En linéarisant les deux termes on obtient :
Soit :
Mais aussi :
En utilisant la formule , on obtient :
Donc :
En regroupant les termes en :
On a alors :
Soit encore :
En utilisant la formule , on obtient :
Ce qui nous permet d'écrire que :
En regroupant les termes :
Ce qui nous donne :
On en déduit donc que :
D'où, avec , on trouve que :
Finalement on obtient :
D'où :
Donc :
Ce qui nous donne :
En linéarisant les deux termes on obtient :
Soit :
Mais aussi :
En utilisant la formule , on obtient :
Donc :
En regroupant les termes en :
On a alors :
Soit encore :
En utilisant la formule , on obtient :
Ce qui nous permet d'écrire que :
En regroupant les termes :
Ce qui nous donne :
On en déduit donc que :
D'où, avec , on trouve que :
Finalement on obtient :