Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

On continue - Exercice 1

20 min
35
Autour de la division euclidienne.
Question 1
Soit α\alpha et β\beta deux nombres complexes.
On considère les deux polynômes AA et BB, à coefficients complexes, suivants :
A(X)=X5+X4+αX3+βX2+5X−2     et     B(X)=X3−2X+1A(X) = X^5 + X^4 + \alpha X^3 + \beta X^2 + 5X - 2 \,\,\,\,\, \mathrm{et} \,\,\,\,\, B(X) = X^3 - 2 X + 1

De manière générale, quelle condition permet d'affirmer qu'un polynôme non nul QQ divise un polynôme PP ?

Correction
La condition, qui permet d'affirmer qu'un polynôme non nul QQ divise un polynôme PP, est que le reste de la division euclidienne de PP par QQ est nul.
Question 2

Effectuer la division euclidienne de AA par BB suivant les puissances décroissantes de XX.

Correction
La division euclidienne de AA par BB, suivant les puissances décroissantes de XX, est :
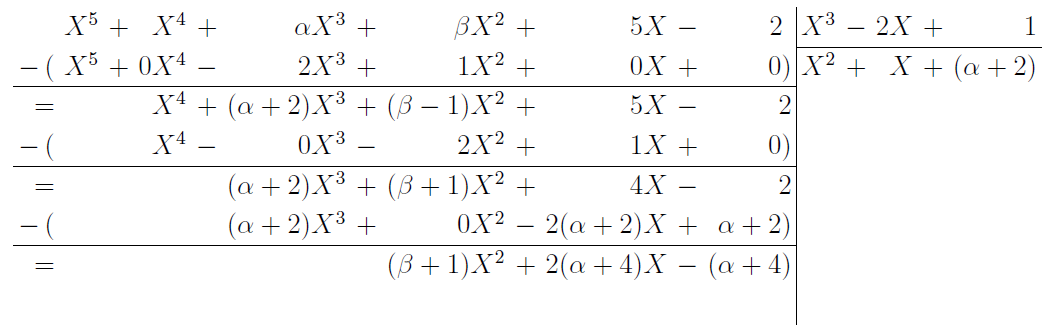
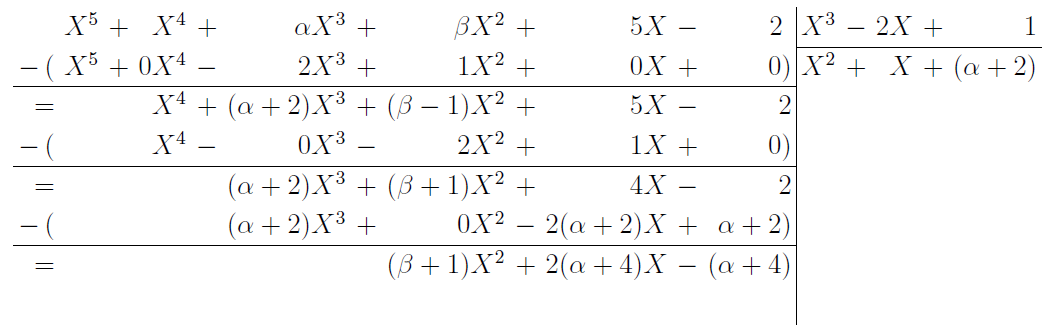
Question 3

Déterminer les valeurs des deux nombres complexes α\alpha et β\beta pour que BB divise AA.

Correction
Pour que BB divise AA, il suffit que :
(β+1)X2+2(α+4)X−(α+4)=0      ⟹      {α=−4β=−1(\beta + 1) X^2 + 2(\alpha+4) X - (\alpha+4) = 0 \,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\, \left\lbrace{\color{red}{ \begin{array}{rcl} \alpha & = & - 4 \\ \beta & = & - 1 \end{array} }} \right.