Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Injective / Surjective : Exercice - Exercice 1
20 min
35
On considère l'application .
Question 1
Etudier l'injectivité de .
Correction
On a :
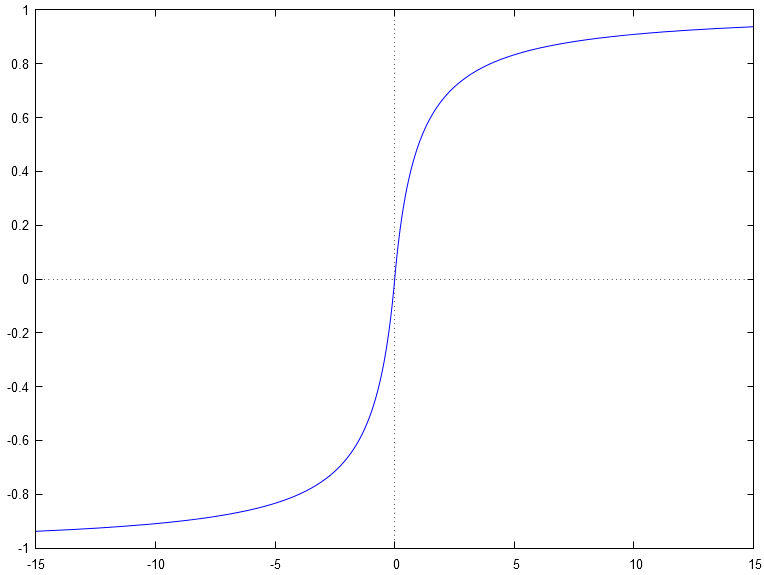
Les deux droites horizontales d'équation respectives et sont donc des asymptotes horizontales au graphe de cette application .
Puis :
si alors et ce qui implique que est croissante sur ;
si alors et ce qui implique que est croissante sur .
Donc est continue et strictement croissante sur . Donc réalise une bijection de dans (attention au sens des crochets pour la surjection). Et de fait, est injective.
En effet, soit et deux réels.
Si on a alors on en déduit que soit .
On a donc démontrer que :
Donc est injective.
Les deux droites horizontales d'équation respectives et sont donc des asymptotes horizontales au graphe de cette application .
Puis :
si alors et ce qui implique que est croissante sur ;
si alors et ce qui implique que est croissante sur .
Donc est continue et strictement croissante sur . Donc réalise une bijection de dans (attention au sens des crochets pour la surjection). Et de fait, est injective.
En effet, soit et deux réels.
Si on a alors on en déduit que soit .
On a donc démontrer que :
Donc est injective.
Question 2
Etudier la surjectivité de .
Correction
On considère l'application .
Donc, l'image conduit à , soit .
Or on a :
Donc impose . Ainsi on obtient l'égalité soit qui est impossible.
On a donc montrer que l'image n'admet pas d'antécédent par et de fait l'application étudiée n'est pas surjective.
Ceci est bien confirmé par le graphe de cette application :
Donc, l'image conduit à , soit .
Or on a :
Donc impose . Ainsi on obtient l'égalité soit qui est impossible.
On a donc montrer que l'image n'admet pas d'antécédent par et de fait l'application étudiée n'est pas surjective.
Ceci est bien confirmé par le graphe de cette application :
