Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Injective / Surjective : Exercice - Exercice 1
20 min
35
On considère l'application .
Sa représentation graphique (son graphe) est :
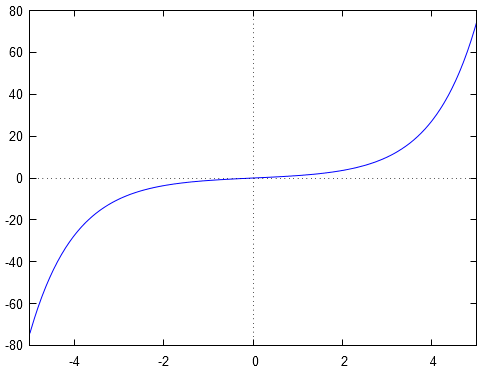 Cette application est connue sous le nom de sinus hyperbolique.
Cette application est connue sous le nom de sinus hyperbolique.
Sa représentation graphique (son graphe) est :

Question 1
Etudier l'injectivité de .
Correction
L'application est continue sur et y est strictement croissante. En vertu du théorème de la bijection, on peut affirmer que est une bijection. Et de fait est injective.
On peut également procéder à partir de l'assertion définition d'une bijection :
Donc, soit . On a alors :
Cette valeur de l'antécédent , associée à l'image réelle , est unique.
L'application argument sinus hyperbolique, notée (parfois égalent notée ) est l'application réciproque de . Sa représentation graphique (en rouge) est la suivante :
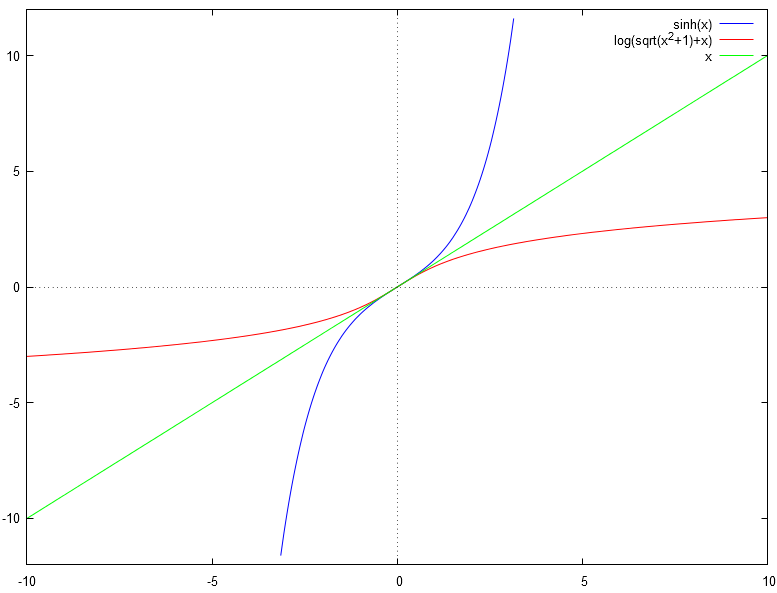 D'ailleurs, on peut également montrer que .
D'ailleurs, on peut également montrer que .
On peut également procéder à partir de l'assertion définition d'une bijection :
Donc, soit . On a alors :
Cette valeur de l'antécédent , associée à l'image réelle , est unique.
L'application argument sinus hyperbolique, notée (parfois égalent notée ) est l'application réciproque de . Sa représentation graphique (en rouge) est la suivante :

Question 2
Etudier la surjectivité de .
Correction
L'application est continue sur et est strictement croissante. En vertu du théorème de la bijection, on peut affirmer que est une bijection. Et de fait est surjective.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.