Cours sur la logique

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Considérons l'assertion $$x \geqslant 2 \Longrightarrow x^2 \geqslant 4$$. Le fait d'avoir $$x \geqslant 2$$ est suffisant pour avoir $$x^2 \geqslant 4$$. Cependant la condition $$x \geqslant 2$$ n'est pas une nécessité pour avoir $$x^2 \geqslant 4$$, car si nous posons $$x=-2$$ (qui ne satisfait pas à $$x \geqslant 2$$) on a pourtant bien $$x^2 \geqslant 4$$. Ainsi pour que $$x^2 \geqslant 4$$ il suffit d'avoir $$x \geqslant 2$$, mais ce n'est pas nécessaire car il y a d'autre moyen d'arriver à la conclusion $$x^2 \geqslant 4$$.
Le fait de constater que $$x^2 \geqslant 4$$ est nécessaire (obligatoire) pour pouvoir affirmer que $$x \geqslant 2$$.

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Voici un exemple classique. Soit $$n \in \mathbb{N}$$. Démontrons que $$n$$ impair $$\Longrightarrow$$ $$n^2$$ impair.
On suppose que $$n$$ est impair, donc l'entier naturel $$n$$ peut s'écrire sous la forme $$n = 2p+1\,\, (p \in \mathbb{N})$$. Dans ce cas on a $$n^2 = (2p+1)^2$$. En développant l'identité remarquable, on obtient $$n^2 = 4p^2+4p+1 = 2(2p^2+2p)+1$$. Posons $$q = 2p^2+2p = 2p(p+1)$$. Comme $$p \in \mathbb{N}$$ cela signifie que $$2p(p+1) \in \mathbb{N}$$, d'où $$q \in \mathbb{N}$$. De fait, $$2q + 1 \in \mathbb{N}$$ et est donc impair. On peut alors conclure que que $$n^2$$ est un nombre entier naturel impair. $${\color{blue}{\blacksquare}}$$ (Ce petit symbole $${\color{blue}{\blacksquare}}$$ signifie simplement que la démonstation est terminée).
Le deuxième méthode pour démontrer l'implication $$P \Longrightarrow Q$$ est de démontrer sa contraposée. En effet, on a l'équivalence logique $$\left(P \Longrightarrow Q\right) \Longleftrightarrow \left(\neg Q \Longrightarrow \neg P \right)$$. Pour illustrer ce principe de démonstration, enisageons le célèbre exemple dans lequep $$P$$ repésente la propposition $$\it{il \, pleut}$$ et $$Q$$ représente la proposition $$\it{je \, prends \, mon \, parapluie}$$. On observe immédiatement que $$P \Longrightarrow Q$$ car si $$\it{il \, pleut}$$ alors $$\it{je \, prends \, mon \, parapluie}$$. Mais nous pouvons également remarquer que "si il ne pleut pas alors je ne prends pas mon parapluie". Ce qui s'identifie à $$\neg Q \Longrightarrow \neg P$$.

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Voici un exemple classique. Soit $$n \in \mathbb{N}$$. Démontrons que $$n^2$$ pair $$\Longrightarrow$$ $$n$$ pair.
Notons par $$P$$ la proposition $$n^2$$ pair, et désignons par $$Q$$ la proposition $$n$$ pair. Nous cherchons à démontrer que $$P \Longrightarrow Q$$. La proposition contraposée $$\neg Q \Longrightarrow \neg P$$ s'identifie à $$n$$ impair $$\Longrightarrow$$ $$n^2$$ impair. La démonstration de la contraposée à été réalisée dans l'exemple précédent. Ce qui achève la démonstration, et nous pouvons affirmer que $$n^2$$ pair $$\Longrightarrow$$ $$n$$ pair. $${\color{blue}{\blacksquare}}$$

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Un exemple classique et pédagogique. Soit $$x$$ et $$m$$ deux nombres réels. Démontrons que l'expression $$f(x) = mx+1$$ garde un signe constant sur $$\mathbb{R}$$ si et seulement si $$m=0$$.
$${\color{green}{ \bullet \,\, } \bf{Implication \,\ directe : la \,\, condition \,\, nécessaire}}$$
Si $$m=0$$ alors $$f(x) = 1 > 0$$. Dans ce cas, pour tout $$x$$ réel, $$\mathrm{signe}(f(x)) = \mathrm{signe}(1)$$ et de fait, pour tout $$x$$ réel, $$\mathrm{signe}(f(x)) = +$$. Ainsi le signe de l'expression $$f(x)$$ est constant sur $$\mathbb{R}$$.
$${\color{green}{\bullet \bullet \,\, } \bf{Implication \,\ réciproque : la \,\, condition \,\, suffisante}}$$
Réciproquement, pour montrer que si l'expression $$f(x)$$ conserve un signe constant alors $$m=0$$ nous allons utiliser la contraposée associée (expliquée ci-avant dans l'implication), à savoir : si $$m \neq 0$$ alors l'expression $$f(x)$$ change de signe.
Donc, si $$m \neq 0$$ alors $$f(x) = m \left( x + \dfrac{1}{m} \right) = m \left( x - \left(-\dfrac{1}{m} \right)\right)$$. On constate alors qu'il y a changement de signe de l'expression $$f(x)$$ lorsque $$x = -\dfrac{1}{m}$$. Par conclusion de la méthode de la contraposée, nous pouvons donc affirmer que si l'expression $$f(x)$$ conserve un signe constant alors $$m=0$$.
$${\color{green}{\bullet \bullet \bullet\,\, } \bf{Conclusion}}$$
Nous avons bien démontrer les deux implications, directe et réciproque, et nous pouvons donc conclure que l'expression $$f(x) = mx+1$$ garde un signe constant sur $$\mathbb{R}$$ si et seulement si $$m=0$$. $${\color{blue}{\blacksquare}}$$

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Démontrons classiquement que le nombre $$\sqrt{2}$$ est un nombre irrationnel.
On rappelle que les nombres irrationnels sont représentés par $$\mathbb{Q}′$$ et sont les nombres dont le développement décimal est infini et non périodique. Autrement dit, un nombre irrationnel est un nombre réel qui n'est pas rationnel, c'est-à-dire qu'il ne peut pas s'écrire sous la forme d'une fraction $$\dfrac{a}{b}$$, où $$a$$ et $$b$$ sont deux entiers relatifs (avec $$b$$ non nul).
Nous cherchons à démontrer que $$\sqrt{2} \notin \mathbb{Q}$$. C'est pourquoi nous allons faire l'hypothèse $$\sqrt{2} \in \mathbb{Q}$$ et chercher une contradiction engendrée.
Si $$\sqrt{2} \in \mathbb{Q}$$ alors $$\sqrt{2} = \dfrac{a}{b}$$, où $$a$$ et $$b$$ sont deux entiers relatifs (avec $$b$$ non nul). On peut supposer que la fraction $$\dfrac{a}{b}$$ soit irréductible. Ceci signifie que les nombres $$a$$ et $$b$$ n'ont pas de diviseur commun, autre que $$1$$. En passant au carré, on a $$\sqrt{2}^2 = \dfrac{a^2}{b^2}$$. Donc $$a^2 = 2 b^2$$. Ceci signifie que $$a^2$$ est pair, ce qui implique $$a$$ est également pair (voir ci-dessus l'exemple de la démonstration par contraposée). Ainsi $$a$$ est un multiple de $$2$$, et on pose $$a=2p$$ avec $$p \in \mathbb{N}$$. On a alors $$4p^2 = 2b^2$$, soit $$2p^2 = b^2$$, et donc $$b^2$$ est une quantité paire, et donc $$b$$ est également pair. D'où $$b = 2q$$ avec $$q \in \mathbb{N}$$. On constate que les deux nombres $$a$$ et $$b$$ sont pairs, donc ils admettent un diviseur commun qui est $$2$$. Cette constatation est une $${\color{blue}{contradiction}}$$ aux fait que la fraction $$\dfrac{a}{b}$$ soit irréductible. Donc notre hypothèse initiale, à savoir $$\sqrt{2} \in \mathbb{Q}, est fausse$$. On en conclut donc que $$\sqrt{2} \notin \mathbb{Q}$$, autrement dit $$\sqrt{2}$$ n'est pas un nombre rationnel, c'est un nombre irrationnel. $${\color{blue}{\blacksquare}}$$

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
Démontrons par récurrence que nous avons la propriété $$P(n)$$, avec $$n \in \mathbb{N}^\star$$ suivante :
$$P(n) : 1+2+\cdots+n= \dfrac{n(n+1)}{2}$$.
$${\color{green}{\bullet \,\, } \bf{Etape \, 1 : L'initialisation}}$$
On vérifie la propriété $$P$$ pour $$n=1$$. On a effectivement :
$$P(1) : 1 = \dfrac{1(1+1)}{2}$$.
$${\color{green}{\bullet \bullet \,\, } \bf{Etape \, 2 : La \,\, transmission}}$$
Soit $$n \in \mathbb{N}$$, tel que $$n > 1$$. On fait la supposition que $$P(n)$$ est vraie, à savoir que nous avons la propriété $$1+2+\cdots+n= \dfrac{n(n+1)}{2}$$. Dans ce cas, examinons la vérité de $$P(n+1)$$. On a donc, sous l'hypothèse que $$P(n)$$ soit vraie :
$$P(n+1) : 1+2+\cdots+n+(n+1)= \dfrac{n(n+1)}{2}+(n+1)$$
A savoir :
$$P(n+1) : 1+2+\cdots+n+(n+1)= (n+1) \left(\dfrac{n}{2}+1\right)$$
Soit :
$$P(n+1) : 1+2+\cdots+n+(n+1)= (n+1) \left(\dfrac{n+2}{2}\right)$$
Soit encore :
$$P(n+1) : 1+2+\cdots+n+(n+1)= \dfrac{(n+1)(n+2)}{2}$$
Qui s'écrit également sous la forme :
$$P({\color{red}{n+1}}) : 1+2+\cdots+n+(n+1)= \dfrac{({\color{red}{n+1}})({\color{red}{n+1}}+1)}{2}$$
On peut donc affirmer que si $$P(n)$$ est vraie alors $$P({\color{red}{n+1}})$$ est également vraie.
$${\color{green}{\bullet \bullet \bullet \,\, } \bf{Etape \, 3 : La \,\, conclusion}}$$
En vertu des axiomes de la récurrence, la propriété $$P(n) : 1+2+\cdots+n= \dfrac{n(n+1)}{2}$$ est vraie pour tout entier naturel $$n \geqslant 1$$, ce qui achève la démonstration $${\color{blue}{\blacksquare}}$$.

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
La négation de $${\color{blue}{\exist}} x \in ]0\,;\,1[, \,\, \sqrt{x} > x$$ est $${\color{red}{\forall}} x \in ]0\,;\,1[, \,\, \sqrt{x} < x$$. Le première assertion est vraie, et donc sa négation, la seconde, est fausse. En effet on vérifie ceci facilement par les graphes représentatifs :

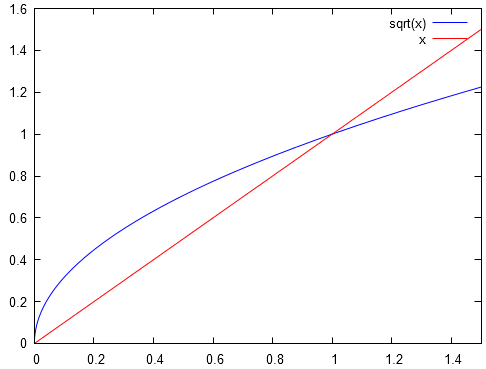
En effet, prenons $$x = 0,5 \in ]0\,;\,1[$$. On a bien $$\sqrt{0,5} > 0,5$$. Donc, il existe bien au moins une valeur de $$x$$ dans l'intervalle $$]0\,;\,1[$$ qui permet d'affirmer que $$\sqrt{x} > x$$.
A ceci, rajoutons la négation (très souvent utile) suivante :
$$\neg \left( {\color{red}{\forall}} x \in E, P(x) \Longrightarrow Q(x) \right) \Longleftrightarrow {\color{blue}{\exist}} x \in E, P(x) \wedge \neg Q(x)$$
$$\blacktriangleright$$ Remarquons que pour démontrer que la proposition $${\color{red}{\forall}} x \in E, \,\, P(x)$$ est fausse, il est possible (et suffisant) de trouver un $${\color{black}{\bf{contre \,\, exemple}}}$$. Autrement dit, trouver un élément $$x$$ de l'ensemble $$E$$ qui rend la propriété $$P(x)$$ vraie.

$${\color{blue}{\,\,\, \sphericalangle \,\,\bf{Exemple :}}}$$
On considère $${\color{red}{\forall}} x \in \mathbb{R}, x^2 > 1 \Longrightarrow x > 1$$. La négation est donc :
$$\neg \left( {\color{red}{\forall}} x \in \mathbb{R}, x^2 > 1 \Longrightarrow x > 1 \right) \Longleftrightarrow {\color{blue}{\exist}} x \in \mathbb{R}, x^2 > 1 \,\, \mathrm{et} \,\, x \leqslant 1$$
On constate que le choix $$x = - 2 \in \mathbb{R}$$ permet de donner la vérité fausse à $${\color{red}{\forall}} x \in \mathbb{R}, x^2 > 1 \Longrightarrow x > 1$$, et de fait offre la vérité vraie à $${\color{blue}{\exist}} x \in \mathbb{R}, x^2 > 1 \,\, \mathrm{et} \,\, x \leqslant 1$$. Donc $$x = - 2 \in \mathbb{R}$$ est $${\color{black}{\bf{contre \,\, exemple}}}$$.