Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Un homicide - Exercice 1
30 min
50
Voici une autre application dans le domaine de la thermique.
Question 1
En hivers, le corps d'une victime a été trouvé sur le lieu du crime à 2H20 du matin, en pleine nuit. Après
une demi-heure la température du corps est de .
A l'heure de la découverte du corps sans vie, la température du corps est de et la température extérieure est de . Le temps est mesuré en minute.
une demi-heure la température du corps est de .
A l'heure de la découverte du corps sans vie, la température du corps est de et la température extérieure est de . Le temps est mesuré en minute.
Quand a eu lieu l'homicide ?
Se rappeler qui dit que la vitesse de refroidissement est proportionnelle à la différence des températures.
Se rappeler qui dit que la vitesse de refroidissement est proportionnelle à la différence des températures.
Correction
L'équation différentielle qui gouverne l'évolution temporelle de la température du corps est donnée par . On a alors l'équation suivante :
On a :
Dans cette équation, est une constante réelle strictement négative. La solution homogène est, avec :
Puis la solution particulière est :
La solution mathématique globale de l'EDO est alors :
Prenons comme origine des temps, l'instant de la découverte du cadavre. On a alors la condition :
Donc on a alors :
De plus, on sait qu'au bout de trente minutes la température du corps est de . Donc on en déduit que :
Ce qui nous donne :
Finalement, la loi de température est donnée par l'expression suivante :
Enfin, pour estimer l'heure de la mort , il suffit de se souvenir que la température corporelle normale est de . Ainsi, on a :
Soit :
Ainsi, on trouve que :
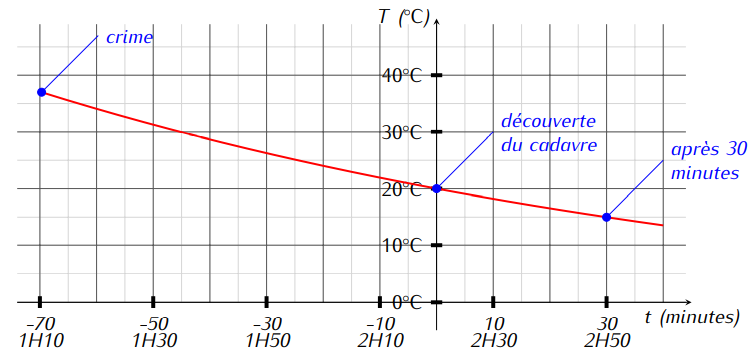
Finalement, l'heure du décès est très voisine de . Graphiquement, cela nous donne :
On a :
Dans cette équation, est une constante réelle strictement négative. La solution homogène est, avec :
Puis la solution particulière est :
La solution mathématique globale de l'EDO est alors :
Prenons comme origine des temps, l'instant de la découverte du cadavre. On a alors la condition :
Donc on a alors :
De plus, on sait qu'au bout de trente minutes la température du corps est de . Donc on en déduit que :
Ce qui nous donne :
Finalement, la loi de température est donnée par l'expression suivante :
Enfin, pour estimer l'heure de la mort , il suffit de se souvenir que la température corporelle normale est de . Ainsi, on a :
Soit :
Ainsi, on trouve que :
Finalement, l'heure du décès est très voisine de . Graphiquement, cela nous donne :
