Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Régime permanent d'un système vibratoire - Exercice 1
40 min
65
Lorsqu'un système physique rentre en vibration, il y a souvent deux régimes de fonctionnement différents. Il y a en premier lieu le régime qualifié de (qui ne dure que très peu de temps) et le régime dit (ou établi). La détermination de ce dernier peut s'effectuer par l'intermédiaire des nombres complexes. La solution générale est, le plus souvent, l'addition des deux solutions de ces deux régimes de fonctionnements différents.
Question 1
On va considérer une approche mécanique, car très visuelle et pragmatique, du modèle.
Dans le référentiel terrestre, considéré comme galiléen, on envisage une masse , constante, qui oscille, horizontalement dans la direction , sous l'action de trois forces :
une force de rappel à la configuration d'équilibre ou le nombre réel strictement positif représente la raideur du rappel.
une force de frottement de type visqueux, donc purement dissipative, et de formulation mathématique ou le nombre réel strictement positif caractérise le frottement lors des oscillations de la masse. C'est l'élément sur la figure suivante.
une force d'excitation extérieure sinusoïdale, de pulsation , de la forme . Le nombre réel est strictement positif. Cette force change de sens périodiquement, et la période des oscillations apparentes est . Cette période d'oscillation est considérée comme étant beaucoup plus petite que la période de rotation de la Terre sur elle même.
Ceci est représenté par la figure suivante :
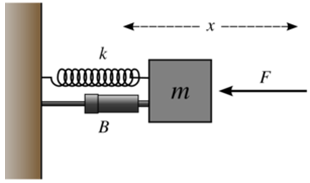
L'application de la deuxième loi de , à la masse , permet d'obtenir la l'équation suivante :
La force d'excitation périodique extérieure va imposer une solution de la forme, également, sinusoïdale. Cependant, la présence d'un frottement dissipatif dans le modèle, entraine une réponse par rapport à l'excitation extérieure. Mathématiquement, ce physique, va se traduire par une différence de phase, , noté . Ainsi, la solution en régime permanent sera donc de la forme mathématique :
Le terme s'appelle l'amplitude et à les mêmes unités que .
Dans le référentiel terrestre, considéré comme galiléen, on envisage une masse , constante, qui oscille, horizontalement dans la direction , sous l'action de trois forces :
une force de rappel à la configuration d'équilibre ou le nombre réel strictement positif représente la raideur du rappel.
une force de frottement de type visqueux, donc purement dissipative, et de formulation mathématique ou le nombre réel strictement positif caractérise le frottement lors des oscillations de la masse. C'est l'élément sur la figure suivante.
une force d'excitation extérieure sinusoïdale, de pulsation , de la forme . Le nombre réel est strictement positif. Cette force change de sens périodiquement, et la période des oscillations apparentes est . Cette période d'oscillation est considérée comme étant beaucoup plus petite que la période de rotation de la Terre sur elle même.
Ceci est représenté par la figure suivante :

L'application de la deuxième loi de , à la masse , permet d'obtenir la l'équation suivante :
La force d'excitation périodique extérieure va imposer une solution de la forme, également, sinusoïdale. Cependant, la présence d'un frottement dissipatif dans le modèle, entraine une réponse par rapport à l'excitation extérieure. Mathématiquement, ce physique, va se traduire par une différence de phase, , noté . Ainsi, la solution en régime permanent sera donc de la forme mathématique :
Le terme s'appelle l'amplitude et à les mêmes unités que .
Le physicien recherche une solution de la forme .
On pose , et de fait . On va donc associer le nombre complexe suivant :
Soit encore :
Ce qui implique que :
De plus, on note :
Ainsi, l'écriture complexe de l'équation modèle est :
En s'imposant les deux conditions d'origines physiques et que , déterminer l'expression de la solution permanente associée à cette situation.
On pose , et de fait . On va donc associer le nombre complexe suivant :
Soit encore :
Ce qui implique que :
De plus, on note :
Ainsi, l'écriture complexe de l'équation modèle est :
En s'imposant les deux conditions d'origines physiques et que , déterminer l'expression de la solution permanente associée à cette situation.
Correction
On a :
En simplifiant par le terme on obtient :
En factorisant par , on trouve que :
Soit :
Comme , on a et . D'où :
Posons , et déterminons son expression. En s'imposant la condition et que , on en déduit que :
Et de fait, on a :
Ceci nous permet d'obtenir :
Comme , on en déduit finalement que :
En simplifiant par le terme on obtient :
En factorisant par , on trouve que :
Soit :
Comme , on a et . D'où :
Posons , et déterminons son expression. En s'imposant la condition et que , on en déduit que :
Et de fait, on a :
Ceci nous permet d'obtenir :
Comme , on en déduit finalement que :