Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La séparation des variables 4 : en Astrophysique - Exercice 1
1 h
90
La méthode de constitue une des méthodes les plus puissantes de résolution des équations différentielles ordinaires (EDO). Cette méthode est particulièrement utilisée en Physique.
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Question 1
Soit un paramètre temporel réel positif ou nul. Dans un système d'unités adapté, le rayon d'un corps auto-gravitant, qui s'effondre sous sa propre masse, obéit à l'équation différentielle suivante :
Les deux conditions initiales associées sont :
On note par la durée nécessaire pour que le corps considéré voit son rayon passer de à . En outre, on donne la valeur de l'intégrale suivante :
Le principe du mécanisme de l'effondrement auto-gravitationnel est illustré sur la figure suivante :
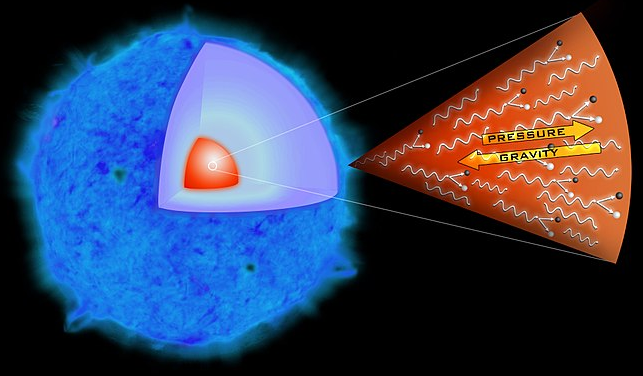
Les deux conditions initiales associées sont :
On note par la durée nécessaire pour que le corps considéré voit son rayon passer de à . En outre, on donne la valeur de l'intégrale suivante :
Le principe du mécanisme de l'effondrement auto-gravitationnel est illustré sur la figure suivante :

Démontrer que l'on a :
Correction
On a l'équation différentielle suivante :
On va la multiplier, des deux côtés, par . On obtient ainsi :
Soit :
De cette égalité de dérivées, on en déduit alors que :
Or, à l'instant initial on a les deux conditions initiales suivantes :
Ce qui nous donne :
Finalement, on obtient bien la relation souhaitée, à savoir :
On va la multiplier, des deux côtés, par . On obtient ainsi :
Soit :
De cette égalité de dérivées, on en déduit alors que :
Or, à l'instant initial on a les deux conditions initiales suivantes :
Ce qui nous donne :
Finalement, on obtient bien la relation souhaitée, à savoir :
Question 2
Donner le signe du terme .
Correction
Le phénomène étudié est un effondrement, par auto-gravitation, d'un corps sphérique. Ceci signifie que le rayon du corps diminue. Donc est une de . En conséquence le signe du terme dérivé est {\color{blue}{négatif}}. D'où :
Question 3
Démontrer que l'équation différentielle démontrer lors de la première question, est de type .
Correction
On a :
Soit :
D'où :
Soit :
D'où :
Question 4
Déterminer l'expression de en fonction de et .
Correction
Nous allons devoir intégrer la relation précédente. On a :
On note par la durée nécessaire pour que le rayon du corps considéré devienne nul. Durant l'évolution temporelle , le rayon du corps passe de . Ainsi, on a l'intégration suivante:
En inversant les bornes de la première intégrale, puis en simplifiant les signes, on obtient :
Il va falloir maintenant faire apparaître l'intégrale donnée dans le sujet. Pour cela écrivons que :
Puis, en écrivant que au sein de la racine carrée présente dans la première intégrale, on arrive à l'écriture suivante :
Soit, avec :
En remarquant que , on obtient :
D'où :
Posons maintenant , ainsi lorsque alors , puis lorsque on a . En conséquence, on obtient :
Or, d'après le sujet, on sait que :
Donc :
Finalement, on obtient :
On note par la durée nécessaire pour que le rayon du corps considéré devienne nul. Durant l'évolution temporelle , le rayon du corps passe de . Ainsi, on a l'intégration suivante:
En inversant les bornes de la première intégrale, puis en simplifiant les signes, on obtient :
Il va falloir maintenant faire apparaître l'intégrale donnée dans le sujet. Pour cela écrivons que :
Puis, en écrivant que au sein de la racine carrée présente dans la première intégrale, on arrive à l'écriture suivante :
Soit, avec :
En remarquant que , on obtient :
D'où :
Posons maintenant , ainsi lorsque alors , puis lorsque on a . En conséquence, on obtient :
Or, d'après le sujet, on sait que :
Donc :
Finalement, on obtient :