La séparation des variables 3 : en Médecine - Exercice 1

On a le problème de $$Cauchy$$ suivant :
$$\left\lbrace \begin{array}{rcl} \dfrac{d \, I}{dt} (t) & = & kI(t) \left( 5000 - I(t) \right) \\ & & \\ I(t = 0) & = & 160 \\ \end{array} \right.$$
Les solutions constantes sont caractérisées par la condition :
$$\dfrac{d \, I}{dt} (t) = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, kI(t) \left( 5000 - I(t) \right) = 0 \,\,\,\, \Longleftrightarrow \,\,\,\, \left\lbrace \begin{array}{rcl} I(t) & = & 0 \\ & & \\ I(t) & = & 5000 \\ \end{array} \right.$$
Ensuite, on constate que l'EDO peut s'écrire comme :
$$\dfrac{dI}{I \left( 5000 - I \right)} = k \, dt$$
On a alors une forme à \og variables séparées \fg. On va donc pouvoir intégrer. On a alors :
$$\int \dfrac{1}{I \left( 5000 - I \right)} dI = \int k \, dt \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{1}{5000}\int \left( \dfrac{1}{I} + \dfrac{1}{5000 - I} \right) dI = k \int dt$$
Soit :
$$\int \dfrac{1}{I} dI - \int \dfrac{-1}{5000 - I} dI = 5000 k \int dt$$
L'intégration est alors immédiate, et on a alors :
$$\ln(I) - \ln(5000 - I) = 5000 k t + C \,\,\,\, (C \in \mathbb{R})$$
D'où :
$$\ln\left( \dfrac{I}{5000 - I} \right) = 5000 k t + C \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{I}{5000 - I} = e^{5000 k t + C}$$
Soit encore :
$$\dfrac{I}{5000 - I} = e^C \, e^{5000 k t} \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{I}{5000 - I} = D \, e^{5000 k t} \,\,\,\, (D = e^C \in \mathbb{R})$$
Ainsi, on en déduit que :
$$I = (5000 - I) D \, e^{5000 k t} \,\,\,\, \Longleftrightarrow \,\,\,\, I = 5000 D \, e^{5000 k t} - ID \, e^{5000 k t}$$
Donc :
$$I + ID \, e^{5000 k t} = 5000 D \, e^{5000 k t} \,\,\,\, \Longleftrightarrow \,\,\,\, I \, \left( 1 + D \, e^{5000 k t} \right) = 5000 D \, e^{5000 k t}$$
Ce qui nous donne :
$$I = \dfrac{5000 D \, e^{5000 k t}}{1 + D \, e^{5000 k t}} \,\,\,\, \Longleftrightarrow \,\,\,\, I = \dfrac{5000}{\dfrac{1}{D} e^{-5000 k t} + 1}$$
Notons par $$\mathcal{D} = \dfrac{1}{D}$$, et on obtient ainsi :
$${\color{blue}{\boxed{I(t) = \dfrac{5000}{\mathcal{D} e^{-5000 k t} + 1} \,\,\,\, (\mathcal{D} \in \mathbb{R}) }}}$$
La condition initiale va nous permettre de déterminer la valeur de la constante réelle $$\mathcal{D}$$. On a alors :
$$I(t=0) = 160 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{5000}{\mathcal{D} e^{-5000 k 0} + 1} = 160 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{5000}{\mathcal{D} + 1} = 160$$
Donc :
$$\dfrac{500}{\mathcal{D} + 1} = 16 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{500}{16} = \mathcal{D} + 1 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{500}{16} - 1 = \mathcal{D} \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{121}{4} = \mathcal{D}$$
Ainsi :
$$I(t) = \dfrac{5000}{\dfrac{121}{4} e^{-5000 k t} + 1} \,\,\,\, \Longleftrightarrow \,\,\,\, I(t) = \dfrac{5000}{\dfrac{121}{4} e^{-5000 k t} + \dfrac{4}{4}}$$
Finalement :
$${\color{blue}{\boxed{I(t) = \dfrac{20000}{121 e^{-5000 k t} + 4} }}}$$
Il nous reste à déterminer la valeur de la constante réelle $$k$$. Pour cela, utilisons la condition indiquée dans le sujet, à savoir \og $$1200$$ le sont sept jours après \fg. On a alors :
$$I(t=7) = 1200 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{20000}{121 e^{-5000 k 7} + 4} = 1200 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{50}{121 e^{-35000 k} + 4} = 3$$
Donc :
$$\dfrac{\dfrac{50}{3} - 4}{121} = e^{-35000 k} \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{38}{363} = e^{-35000 k} \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{363}{38} = e^{35000 k}$$
D'où :
$$\ln \left(\dfrac{363}{38} \right) = 35000 k \,\,\,\, \Longleftrightarrow \,\,\,\, k = \dfrac{\ln \left(\dfrac{363}{38} \right)}{35000} \,\,\,\, \Longleftrightarrow \,\,\,\, 5000kt = \dfrac{\ln \left(\dfrac{363}{38} \right)}{7}t$$
Finalement, la loi d'évolution temporelle de $$I$$ est :
$${\color{red}{\boxed{I(t) = \dfrac{20000}{121 e^{-\frac{\ln \left(\frac{363}{38} \right)}{7}t} + 4} }}}$$
Si $$80\%$$ de la population est infectée, cela correspond à $$4000$$ personnes. Donc $$I(t_{80}) = 4000$$. On a alors :
$$\dfrac{20000}{121 e^{-\frac{\ln \left(\frac{363}{38} \right)}{7}t_{80}} + 4} = 4000 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{5}{121 e^{-\frac{\ln \left(\frac{363}{38} \right)}{7}t_{80}} + 4} = 1$$
Donc :
$$5 = 121 e^{-\frac{\ln \left(\frac{363}{38} \right)}{7}t_{80}} + 4 \,\,\,\, \Longleftrightarrow \,\,\,\, \dfrac{1}{121} = e^{-\frac{\ln \left(\frac{363}{38} \right)}{7}t_{80}}$$
Ainsi :
$$121 = e^{\frac{\ln \left(\frac{363}{38} \right)}{7}t_{80}} \,\,\,\, \Longleftrightarrow \,\,\,\, \ln(121) = \frac{\ln \left(\dfrac{363}{38} \right)}{7}t_{80} \,\,\,\, \Longleftrightarrow \,\,\,\, 7 \dfrac{\ln(121)}{\ln \left(\dfrac{363}{38} \right)} = t_{80}$$
Ce qui nous donne numériquement :
$${\color{red}{\boxed{t_{80} \simeq 15 \,\, jours }}}$$

Il est impossible de trouver un nombre de jour fini pour lequel l'infection touche $$100\%$$ de la population. En fait, mathématiquement, la réponse est l'infinie. Donc :
$${\color{red}{\boxed{t_{100} \longleftrightarrow + \infty}}}$$
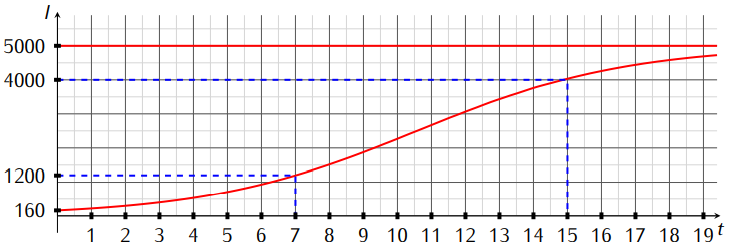
Graphiquement, on a :