Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La séparation des variables 2 : en Mécanique - Exercice 1
50 min
75
La méthode de constitue une des méthodes les plus puissantes de résolution des équations différentielles ordinaires (EDO). Cette méthode est particulièrement utilisée en Physique.
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Question 1
Soit un paramètre temporel réel positif ou nul. Une goutte d'eau, de masse constante , et de taille inférieure à deux millimètres, peut-être considérée comme restant sphérique lors de sa chute verticale dans l'air.
En outre, au regard des régimes de vitesses atteintes par une telle goutte lors de sa chute, les forces de frottement qu'elle subit sont modélisées par l'expression, dite "", à savoir . Dans cette expression est une constante réelle, strictement positive, dont l'origine est purement géométrique.
Sur la hauteur de chute, on considère que les effet de pesanteur terrestre sont constants (uniformes et stationnaires). Ainsi la valeur de est fixe.
La goutte se détache de son nuage créateur sans vitesse, puis débute sa chute. Sous l'effet des frottements son accélération diminue, et donc sa vitesse atteint une valeur limite maximale, notée .
Il résulte de cette modélisation élémentaire, mais réaliste, une équation différentielle en :
Soit encore :
On rappelle que l'on a la primitive suivante :
Dans cette formule, représente la fonction "argument de la tangente hyperbolique", qui est la fonction réciproque, sur , de la fonction {\color{red}{\textbf{tangente hyperbolique}}}.
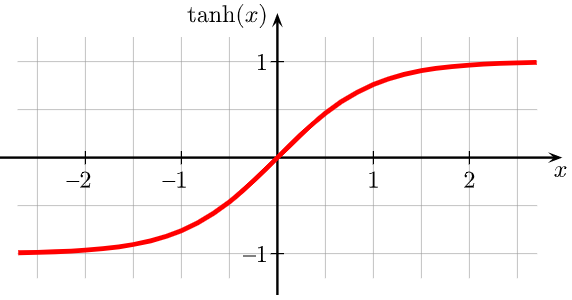
En outre, on donne également le graphe de la fonction réelle univariée, dérivable sur , , notée, :
En outre, au regard des régimes de vitesses atteintes par une telle goutte lors de sa chute, les forces de frottement qu'elle subit sont modélisées par l'expression, dite "", à savoir . Dans cette expression est une constante réelle, strictement positive, dont l'origine est purement géométrique.
Sur la hauteur de chute, on considère que les effet de pesanteur terrestre sont constants (uniformes et stationnaires). Ainsi la valeur de est fixe.
La goutte se détache de son nuage créateur sans vitesse, puis débute sa chute. Sous l'effet des frottements son accélération diminue, et donc sa vitesse atteint une valeur limite maximale, notée .
Il résulte de cette modélisation élémentaire, mais réaliste, une équation différentielle en :
Soit encore :
On rappelle que l'on a la primitive suivante :
Dans cette formule, représente la fonction "argument de la tangente hyperbolique", qui est la fonction réciproque, sur , de la fonction {\color{red}{\textbf{tangente hyperbolique}}}.
En outre, on donne également le graphe de la fonction réelle univariée, dérivable sur , , notée, :

Démontrer que l'équation différentielle considérée est .
Correction
On a l'équation différentielle suivante, avec :
Avec . Il s'agit d'une EDO de . En effet, on peut écrire que :
Avec . Il s'agit d'une EDO de . En effet, on peut écrire que :
Question 2
Déterminer l'expression de la vitesse limite .
Correction
Lorsque la vitesse atteint sa valeur limite alors celle dernière reste constante, et de fait ne varie plus, et en conséquence sa dérivée temporelle est nulle. Donc :
Donc :
Comme est une quantité physique strictement positive, on en déduit finalement que :
Donc :
Comme est une quantité physique strictement positive, on en déduit finalement que :
Question 3
Déterminer l'expression de la fonction vitesse de la goutte .
Correction
On a alors :
Soit :
Ce qui nous donne :
Comme est une constante réelle, on a alors :
Posons . Dans ce cas, on obtient :
En intégrant, on obtient :
Soit une constante réelle. On a alors :
On pose . Dans ce cas, on a :
En prenant la tangente hyperbolique des deux membres de cette dernière équation, on obtient :
Donc :
Or, à l'instant initial , la goutte d'eau se détache de son nuage créateur à vitesse nulle. Donc . Ainsi, on a :
Comme , on en déduit que :
Finalement, on obtient la loi temporelle de la vitesse de la goutte suivante :
Soit :
Ce qui nous donne :
Comme est une constante réelle, on a alors :
Posons . Dans ce cas, on obtient :
En intégrant, on obtient :
Soit une constante réelle. On a alors :
On pose . Dans ce cas, on a :
En prenant la tangente hyperbolique des deux membres de cette dernière équation, on obtient :
Donc :
Or, à l'instant initial , la goutte d'eau se détache de son nuage créateur à vitesse nulle. Donc . Ainsi, on a :
Comme , on en déduit que :
Finalement, on obtient la loi temporelle de la vitesse de la goutte suivante :