Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La méthode de la variation de la constante - Exercice 1
1 h
90
Question 1
Résolvez l'équation différentielle suivante :
Correction
On a donc :
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire :
Par dérivation, on peut écrire que :
Soit encore :
Ce qui nous donne encore :
Donc, on trouve que :
L'équation différentielle linéaire du premier ordre considérée prend donc la forme suivante :
En simplifiant, on trouve que :
Soit encore :
Ce qui peut encore s'écrire :
Donc, en en déduit immédiatement que :
Donc, on a :
Finalement :
La solution globale est donc la somme de la solution homogène et de la solution particulière trouvée , à savoir :
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire :
Par dérivation, on peut écrire que :
Soit encore :
Ce qui nous donne encore :
Donc, on trouve que :
L'équation différentielle linéaire du premier ordre considérée prend donc la forme suivante :
En simplifiant, on trouve que :
Soit encore :
Ce qui peut encore s'écrire :
Donc, en en déduit immédiatement que :
Donc, on a :
Finalement :
La solution globale est donc la somme de la solution homogène et de la solution particulière trouvée , à savoir :
Question 2
Résolvons l'équation différentielle suivante :
avec la condition particulière et .
avec la condition particulière et .
Correction
On a donc :
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire :
Par dérivation, on peut écrire que :
L'équation différentielle linéaire du premier ordre considérée prend donc la forme suivante :
Soit encore :
En développant, on obtient :
En simplifiant, on trouve que :
Or, si alors il est possible de simplifier par . Sous cette condition de , on trouve que :
D'où :
En intégrant, on trouve que :
Donc, on a :
Finalement :
La solution globale est donc la somme de la solution homogène et de la solution particulière trouvée , à savoir :
Soit encore :
Finalement, on obtient la solution globale suivante :
La condition particulière s'écrit :
satisfaisant à la condition particulière est donc :
Graphiquement, cette solution est :
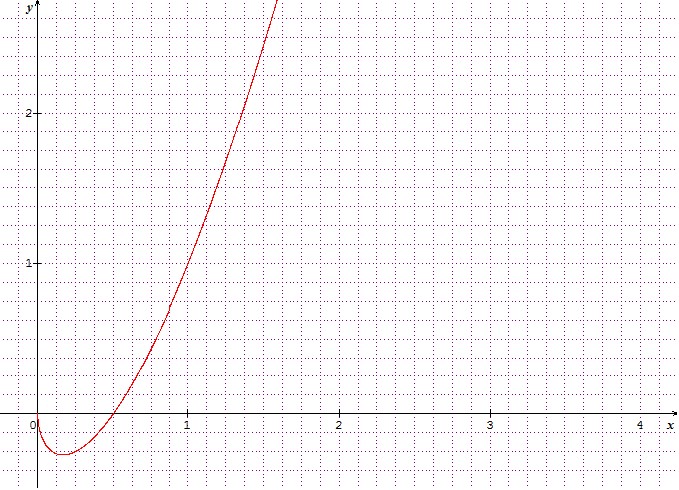
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire :
Par dérivation, on peut écrire que :
L'équation différentielle linéaire du premier ordre considérée prend donc la forme suivante :
Soit encore :
En développant, on obtient :
En simplifiant, on trouve que :
Or, si alors il est possible de simplifier par . Sous cette condition de , on trouve que :
D'où :
En intégrant, on trouve que :
Donc, on a :
Finalement :
La solution globale est donc la somme de la solution homogène et de la solution particulière trouvée , à savoir :
Soit encore :
Finalement, on obtient la solution globale suivante :
La condition particulière s'écrit :
satisfaisant à la condition particulière est donc :
Graphiquement, cette solution est :
