Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Evolution de population - Exercice 1
30 min
45
Les équations différentielles ordinaire (en langage mathématique on les dénomme EDO), s'appliquent à de multiples domaines. Citons par exemples : Physique, Chimie, Biologie, Météorologie, Finance ...
Question 1
On étudie en laboratoire l'évolution, au cours du temps , d'une population de rongeurs, que l'on note . On adopte la notation pour la dérivée temporelle première de .
Un premier modèle théorique prévoit que vérifie l'équation différentielle suivante :
Résoudre l'équation différentielle .
Résoudre l'équation différentielle .
Correction
On a :
Il s'agit d'une EDO homogène linéaire du premier ordre, à coefficients constants, dont la solution est :
La condition initiale, définissant le problème de , est :
Finalement :
Il s'agit d'une EDO homogène linéaire du premier ordre, à coefficients constants, dont la solution est :
La condition initiale, définissant le problème de , est :
Finalement :
Question 2
À partir de quel instant la population dépassera-t-elle rongeurs ?
Correction
On a la condition suivante :
Finalement, le sens de variation (monotonie et croissance sur ) de nous permet d'écrire :
Finalement, le sens de variation (monotonie et croissance sur ) de nous permet d'écrire :
Question 3
En réalité, un prédateur empêche une telle croissance de la population en tuant certains rongeurs. En intégrant le rôle des prédateurs dans le modèle, on aboutit à une nouvelle équation différentielle :
Avec . En outre, on supposera qu'à chaque instant . Le temps est exprimé en années et en centaines d'individus.
On définit alors la fonction . Montrer que vérifie l'équation différentielle :
Avec .
Avec . En outre, on supposera qu'à chaque instant . Le temps est exprimé en années et en centaines d'individus.
On définit alors la fonction . Montrer que vérifie l'équation différentielle :
Avec .
Correction
On pose . Dans ce cas, on a :
Ce qui nous permet d'écrire que :
En multipliant par , on obtient :
Finalement, en multipliant par , on trouve que :
Ce qui nous permet d'écrire que :
En multipliant par , on obtient :
Finalement, en multipliant par , on trouve que :
Question 4
Résoudre puis en déduire l'expression de la population .
Correction
La solution homogène associée est notée , et correspond à la solution de l'équation suivante :
Donc, avec :
Puis, notons par la solution particulière. Comme le second membre est , on va donc poser . Donc . Dans ce cas, l'équation différentielle étudiée devient :
Soit :
Ainsi, la solution globale est :
Cependant, la condition initiale qui définie le problème de \textit{Cauchy} est . Donc :
La solution globale de notre problème est donc :
Finalement, on aboutit à la solution suivante :
Donc, avec :
Puis, notons par la solution particulière. Comme le second membre est , on va donc poser . Donc . Dans ce cas, l'équation différentielle étudiée devient :
Soit :
Ainsi, la solution globale est :
Cependant, la condition initiale qui définie le problème de \textit{Cauchy} est . Donc :
La solution globale de notre problème est donc :
Finalement, on aboutit à la solution suivante :
Question 5
Dans ce modèle, comment se comporte la taille de la population de rongeurs lorsque ?
Correction
Lorsque on en déduit que . Et dans ce cas, on trouve que :
La population de rongeurs étudiée se stabilisera à individus.
Les fonctions logistiques sont initialement créées par le mathématicien belge Pierre François Verhulst. Chargé par son professeur Adolphe Quetelet, statisticien belge également, d'étudier un modèle d'évolution de population qui ne soit pas exponentiel, il propose en trois publications (1838, 1845 et 1847) un nouveau modèle tenant compte d'un frein dans le développement de la population et prouve que ce modèle est cohérent avec l'évolution de la population en Belgique et en France jusqu'en 1833. Ces courbes ont la forme d'un S ce qui fait qu'elles sont parfois appelées sigmoïdes. Dans notre problème de rongeurs, la courbe solution est la suivante :
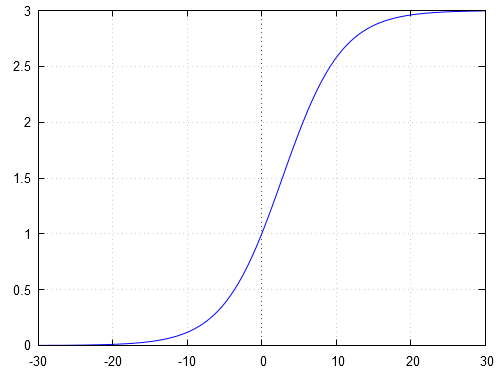
La population de rongeurs étudiée se stabilisera à individus.
Les fonctions logistiques sont initialement créées par le mathématicien belge Pierre François Verhulst. Chargé par son professeur Adolphe Quetelet, statisticien belge également, d'étudier un modèle d'évolution de population qui ne soit pas exponentiel, il propose en trois publications (1838, 1845 et 1847) un nouveau modèle tenant compte d'un frein dans le développement de la population et prouve que ce modèle est cohérent avec l'évolution de la population en Belgique et en France jusqu'en 1833. Ces courbes ont la forme d'un S ce qui fait qu'elles sont parfois appelées sigmoïdes. Dans notre problème de rongeurs, la courbe solution est la suivante :
