Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Circuit électrique RLC (EDO d'ordre deux) - Exercice 1
1 h
90
Les équations différentielles d'ordre deux, en Physique, traduisent des effets dynamiques. En voici un exemple en électricité. C'est un exercice classique qu'il faut impérativement maîtriser.
Question 1
On considère le circuit usuel RLC suivant :
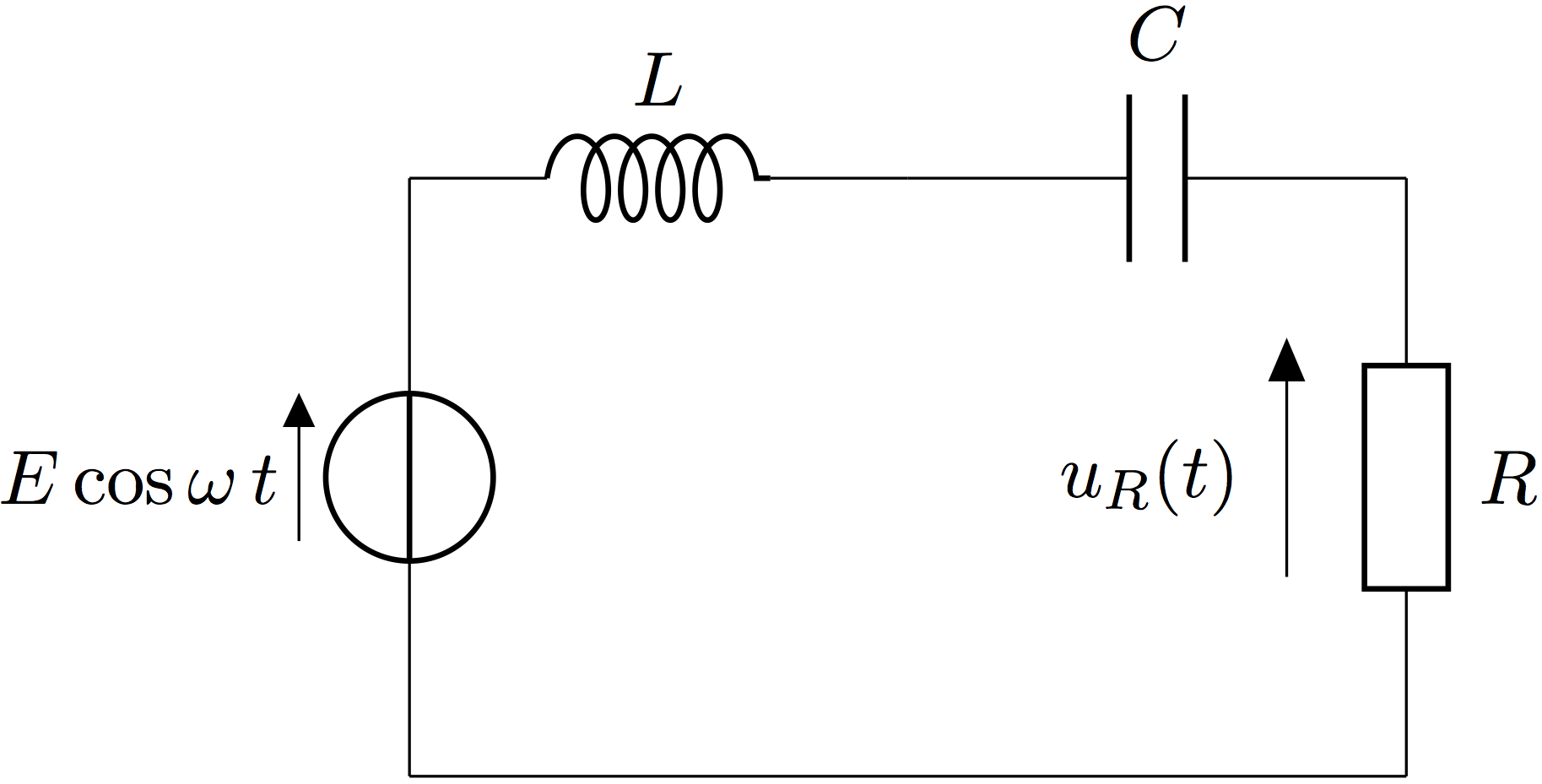
A l'aide de la loi des mailles (encore appelée deuxième lois de et qui nous apprend que dans une maille quelconque d'un réseau, et dans le cadre de l'approximation des régimes quasi stationnaires, et à condition que les variations de flux magnétique à travers la maille soient négligeables, la somme des tensions réceptrices est égale à la sommes des tensions génératrices), on établit l'équation différentielle (ordinaire) qui gouverne l'évolution temporelle de la tension aux bornes du condensateur. On obtient alors :
Par , on pose :
Puis, par d'écriture, on pose :
L'équation différentielle ordinaire du circuit \og RLC série \fg prend alors la forme (modèle) suivante :
Une telle équation différentielle ordinaire modélise un "".
Les deux conditions initiales associées à ce circuit sont les suivantes :
La première de ces deux conditions initiales traduit, qu'au départ, le condensateur est déchargé (donc sans charges électriques sur ses armatures), et la seconde traduit que le circuit électrique ne transfert pas de courant électrique (donc pas de transfert électronique en cours à l'instant initial).

A l'aide de la loi des mailles (encore appelée deuxième lois de et qui nous apprend que dans une maille quelconque d'un réseau, et dans le cadre de l'approximation des régimes quasi stationnaires, et à condition que les variations de flux magnétique à travers la maille soient négligeables, la somme des tensions réceptrices est égale à la sommes des tensions génératrices), on établit l'équation différentielle (ordinaire) qui gouverne l'évolution temporelle de la tension aux bornes du condensateur. On obtient alors :
Par , on pose :
Puis, par d'écriture, on pose :
L'équation différentielle ordinaire du circuit \og RLC série \fg prend alors la forme (modèle) suivante :
Une telle équation différentielle ordinaire modélise un "".
Les deux conditions initiales associées à ce circuit sont les suivantes :
La première de ces deux conditions initiales traduit, qu'au départ, le condensateur est déchargé (donc sans charges électriques sur ses armatures), et la seconde traduit que le circuit électrique ne transfert pas de courant électrique (donc pas de transfert électronique en cours à l'instant initial).
Déterminer le discriminant associée à l'équation différentielle homogène.
Correction
Le discriminant associée à l'équation différentielle homogène est :
On constate que . Donc le signe du discriminant est le même que celui tu terme .
On constate que . Donc le signe du discriminant est le même que celui tu terme .
Question 2
Déterminer les solutions homogènes possibles.
Correction
Il y a donc trois cas possibles concernant les solutions homogènes possibles. On a alors :
Les deux racines réelles distinctes de l'équation caractéristique sont :
Soit :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Soit :
Soit encore :
La racine réelle (double) de l'équation caractéristique est :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Soit :
Les deux racines complexes conjuguées, donc distinctes, de l'équation caractéristique considéré sont :
Soit :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Les deux racines réelles distinctes de l'équation caractéristique sont :
Soit :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Soit :
Soit encore :
La racine réelle (double) de l'équation caractéristique est :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Soit :
Les deux racines complexes conjuguées, donc distinctes, de l'équation caractéristique considéré sont :
Soit :
Dans ce cas, avec et qui sont deux nombres réels, on a :
Question 3
Déterminer la solution particulière .
Correction
Le second membre de l'EDO étudiée est , c'est pourquoi on va choisir une solution particulière de la forme :
De suite, on a :
L'EDO proposée devient :
Soit :
D'où :
Donc :
Ce qui nous permet d'écrire que :
Donc :
Ce qui nous donne :
Ce qui implique que :
Ainsi :
Donc la solution particulière est donc donnée par l'expression suivante :
De suite, on a :
L'EDO proposée devient :
Soit :
D'où :
Donc :
Ce qui nous permet d'écrire que :
Donc :
Ce qui nous donne :
Ce qui implique que :
Ainsi :
Donc la solution particulière est donc donnée par l'expression suivante :
Question 4
Déterminer la solution générale physique lorsque l'on a .
Correction
La condition {\color{red}{}} est strictement identique à {\color{red}{}}. Ceci signifie que :
Donc la solution globale mathématique recherchée est donnée par :
Donc :
Il nous faut maintenant déterminer les deux constantes réelles et à l'aide des deux conditions initiales. On a alors, avec la première condition initiale , et en se souvenant que , et :
Donc :
Puis, par dérivation temporelle, on a :
La seconde condition initiale est . Donc, on obtient :
Soit encore :
En factorisant par , on obtient :
Dès lors :
On obtient donc :
En réduisant au même dénominateur :
Soit :
D'où :
Finalement, après factorisation, {\color{red}{\textbf{la solution globale physique}}} recherchée est donnée par l'expression suivante :
Donc la solution globale mathématique recherchée est donnée par :
Donc :
Il nous faut maintenant déterminer les deux constantes réelles et à l'aide des deux conditions initiales. On a alors, avec la première condition initiale , et en se souvenant que , et :
Donc :
Puis, par dérivation temporelle, on a :
La seconde condition initiale est . Donc, on obtient :
Soit encore :
En factorisant par , on obtient :
Dès lors :
On obtient donc :
En réduisant au même dénominateur :
Soit :
D'où :
Finalement, après factorisation, {\color{red}{\textbf{la solution globale physique}}} recherchée est donnée par l'expression suivante :
Question 5
On se place maintenant dans le cas particulier pour lequel {\color{red}{}}. Déterminer, dans ce cas précis, l'expression de la tension électrique aux bornes du condensateur .
Correction
Si , alors et .
Dans ce cas, on trouve que :
En simplifiant on obtient :
Puis, en factorisant, on trouve que :
De plus, on a :
Ce qui nous donne :
Finalement, on obtient :
Dans ce cas, on trouve que :
En simplifiant on obtient :
Puis, en factorisant, on trouve que :
De plus, on a :
Ce qui nous donne :
Finalement, on obtient :
Question 6
Dans l'expression précédemment trouvée de , donner l'expression de la partie qui modélise les oscillations transitoires. Puis, donner l'expression de , qui modélise les oscillations électriques établies.
Correction
Dans la solution précédente, le terme associé aux oscillations transitoires est celui qui contient l'exponentielle décroissante. Donc il est donné par :
Puis, le terme du régime d'oscillations établies est donc donné par l'expression :
Puis, le terme du régime d'oscillations établies est donc donné par l'expression :
Question 7
On pose maintenant :
volts ;
radians par seconde ;
par seconde.
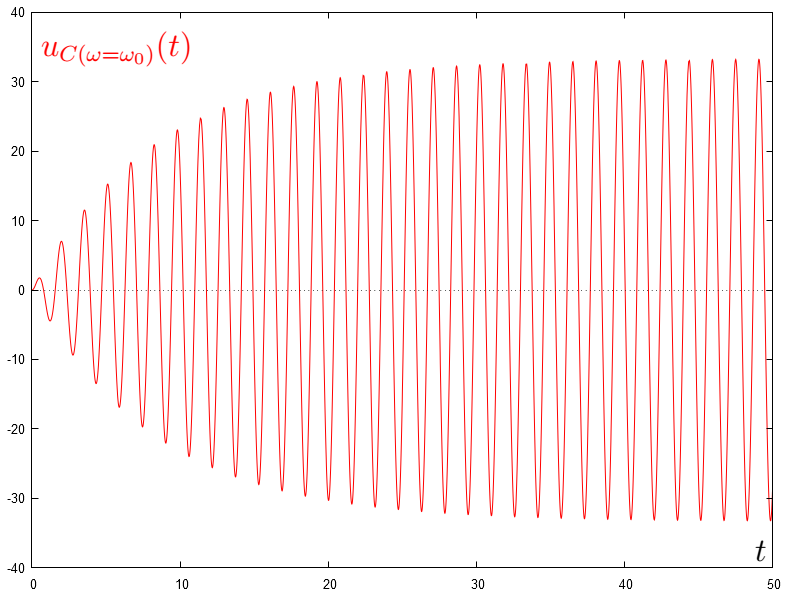
Tracer, pour les cinquante premières secondes, le graphique de la tension électrique qui existe aux bornes du condensateur.
volts ;
radians par seconde ;
par seconde.
Tracer, pour les cinquante premières secondes, le graphique de la tension électrique qui existe aux bornes du condensateur.
Correction
Lorsque l'on pose volts, puis radians par seconde et enfin par seconde, on obtient (pour les cinquante premières secondes) le graphique suivant :