Pour vérifier les savoir-faire ! - Exercice 1

On a :
$$\left(1 + \sin(x)\right)^x = e^{\ln\left( \left(1 + \sin(x)\right)^x \right)} = e^{x\ln\left( 1 + \sin(x) \right)} = e^{x\ln\left( 1 + x - \frac{x^3}{6} + o(x^4)\right)} = e^{x\ln\left( 1 + x - \frac{x^3}{6} \right)} + o(x^5)$$
Or :
$$\ln(1+X) = X - \dfrac{1}{2}X^2 + \dfrac{1}{3}X^3 - \dfrac{1}{4}X^4 + o(X^4)$$
Comme $$\lim_{x \longrightarrow 0} \left( x - \frac{x^3}{6} \right) = 0$$ on va pouvoir poser $$X = x - \frac{x^3}{6}$$. On a alors :
$$\ln\left( 1 + x - \frac{x^3}{6} \right) = \left( x - \frac{x^3}{6} \right) - \dfrac{1}{2}\left( x - \frac{x^3}{6} \right)^2 + \dfrac{1}{3}\left( x - \frac{x^3}{6} \right)^3 - \dfrac{1}{4}\left( x - \frac{x^3}{6} \right)^4 + o(x^{12})$$
En se limitant à l'ordre $$4$$, on obtient :
$$\ln\left( 1 + x - \frac{x^3}{6} \right) = x - \frac{x^3}{6} - \dfrac{1}{2}\left( x^2 - \frac{2x^4}{6} \right) + \dfrac{1}{3}\left( x \right)^3 - \dfrac{1}{4}\left( x \right)^4 + o(x^{4})$$
Soit :
$$\ln\left( 1 + x - \frac{x^3}{6} \right) = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \frac{x^3}{6} + \frac{2x^4}{12} - \dfrac{x^4}{4} + o(x^{4})$$
Donc :
$$\ln\left( 1 + x - \frac{x^3}{6} \right) = x - \dfrac{x^2}{2} + \dfrac{x^3}{6} - \frac{x^4}{12} + o(x^{4})$$
Ainsi :
$$x\ln\left( 1 + x - \frac{x^3}{6} \right) = x^2 - \dfrac{x^3}{2} + \dfrac{x^4}{6} - \frac{x^5}{12} + o(x^{5})$$
On en déduit donc que :
$$\left(1 + \sin(x)\right)^x = e^{x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12}} + o(x^5)$$
Cependant, on sait également que :
$$e^X = 1 + X + \dfrac{1}{2}X^2 + o(X^2)$$
Comme $$\lim_{x \longrightarrow 0} \left( x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12} \right) = 0$$ on va pouvoir poser $$X = x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12}$$. On a alors :
$$e^{x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12}} = 1 + x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12} + \dfrac{1}{2}\left( x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12} \right)^2 + o(x^{10})$$
A l'ordre $$5$$, on obtient :
$$e^{x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12}} = 1 + x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12} + \dfrac{1}{2}x^4 - \frac{x^5}{2} + o(x^5)$$
D'où :
$$e^{x^2 - \frac{x^3}{2} + \frac{x^4}{6} - \frac{x^5}{12}} = 1 + x^2 - \frac{x^3}{2} + \frac{2x^4}{3} - \frac{7x^5}{12} + o(x^5)$$
On en déduit donc que :
$$\left(1 + \sin(x)\right)^x = 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{7}{12}x^5 + o(x^5)$$
Puis, on a :
$$(1+x)^{\sin(x)} = e^{\ln\left( (1+x)^{\sin(x)} \right)} = e^{\sin(x)\ln\left( 1+x \right)}$$
Avec :
$$\sin(x)\ln(1+x) = \left( x - \dfrac{1}{6}x^3 + o(x^4) \right) \times \left( x - \dfrac{1}{2}x^2 + \dfrac{1}{3}x^3 - \dfrac{1}{4}x^4 + o(x^4) \right)$$
Soit, jusqu'à l'ordre $$5$$ :
$$\sin(x)\ln(1+x) = x^2 - \dfrac{1}{2}x^3 + \dfrac{1}{3}x^4 - \dfrac{1}{4}x^5 - \dfrac{1}{6}x^4 + \dfrac{1}{12}x^5 + o(x^5)$$
Ce qui nous donne :
$$\sin(x)\ln(1+x) = x^2 - \dfrac{1}{2}x^3 + \dfrac{1}{6}x^4 - \dfrac{1}{6}x^5 + o(x^5)$$
Ainsi :
$$(1+x)^{\sin(x)} = e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 + o(x^5)} = e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5} + o(x^5)$$
Or, on sait que :
$$e^X = 1 + X + \frac{1}{2}X^2 + o(X^2)$$
Comme $$\lim_{x \longrightarrow 0} \left( x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 \right) = 0$$ on va pouvoir poser $$X = x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5$$. On a alors :
$$e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5} = 1 + x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 + \frac{1}{2}\left( x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 \right)^2 + o(x^{10})$$
En se limitant à l'ordre $$5$$, on obtient :
$$e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5} = 1 + x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 + \frac{1}{2}\left( x^2 - \frac{1}{2}x^3 \right)^2 + o(x^{5})$$
A savoir :
$$e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5} = 1 + x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5 + \frac{1}{2}x^4 - \frac{1}{2}x^5 + o(x^{5})$$
Soit encore :
$$e^{x^2 - \frac{1}{2}x^3 + \frac{1}{6}x^4 - \frac{1}{6}x^5} = 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{2}{3}x^5 + o(x^{5})$$
Ce qui nous permet d'écrire que :
$$(1+x)^{\sin(x)} = 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{2}{3}x^5 + o(x^{5})$$
Par soustraction, on trouve que :
$$f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} = 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{7}{12}x^5 + o(x^5) - \left( 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{2}{3}x^5 + o(x^{5}) \right)$$
D'où :
$$f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} = 1 + x^2 - \frac{1}{2}x^3 + \frac{2}{3}x^4 - \frac{7}{12}x^5 - 1 - x^2 + \frac{1}{2}x^3 - \frac{2}{3}x^4 + \frac{2}{3}x^5 + o(x^{5})$$
Ce qui nous donne :
$$f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} = - \frac{7}{12}x^5 + \frac{2}{3}x^5 + o(x^{5})$$
Soit encore :
$$f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} = \left( \frac{2}{3} - \frac{7}{12} \right)x^5 + o(x^{5}) = \left( \frac{8}{12} - \frac{7}{12} \right)x^5 + o(x^{5}) = \left( \frac{8-7}{12} \right)x^5 + o(x^{5})$$
On trouve alors que :
$$f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} = \frac{1}{12}x^5 + o(x^{5})$$
Finalement, un équivalent simple, au voisinage de $$0$$, de $$f(x)$$ est :
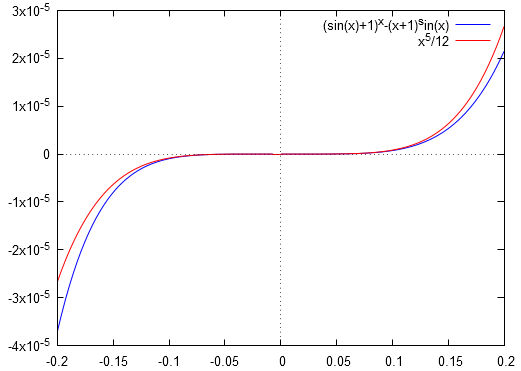
$${\color{red}{\boxed{ f(x) = \left(1 + \sin(x)\right)^x - (1+x)^{\sin(x)} \underset{0}{\sim} \frac{1}{12}x^5 }}}$$
Graphiquement, on observe bien cela :