Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Insupportable ! - Exercice 1
45 min
70
Un exercice complet !
Question 1
Parfois il faut de la patience et de la réflexion.
Déterminer, au voisinage de , le D.L. à l'ordre de .
Correction
La fonction considérée est :
Soit :
Si on pose on constate que , mais également que :
Or :
Donc :
De plus, on a :
Donc :
On en déduit donc que :
D'où :
Finalement :
Graphiquement, on observe que :
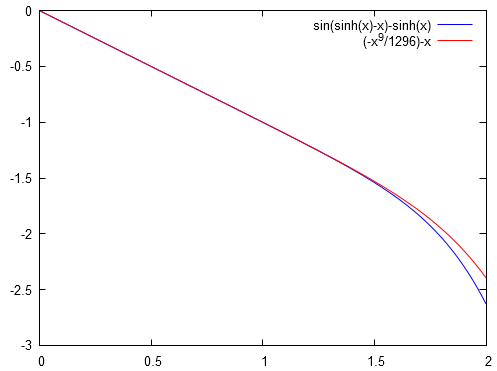
On constate bien l'accord au voisinage de .
Soit :
Si on pose on constate que , mais également que :
Or :
Donc :
De plus, on a :
Donc :
On en déduit donc que :
D'où :
Finalement :
Graphiquement, on observe que :

On constate bien l'accord au voisinage de .