A la limite du supportable ! - Exercice 1

Nous allons réaliser un D.L. de $$f$$ en $$0$$, à l'ordre $$1$$. Ainsi nous pourrons conclure sans difficulté sur la valeur numérique réelle de $$\ell$$. Comme le dénominateur est d'ordre $$7$$, nous allons donc réaliser un D.L. du numérateur de $$f$$ en $$0$$, à l'ordre $$8$$.
La fonction $$f$$ présente des produits et des puissances nous allons pratiquer les équivalences suivantes :
$$\bullet \,\, \sin(x) \underset{0}{\sim} x \,\,\,\, \Longrightarrow \,\,\,\, \sin^3(x) \underset{0}{\sim} x^3 \,\,\,\, \Longrightarrow \,\,\,\, \sin^3(x) = (x + o(x^2))^3$$
$$\bullet \,\, \ln(1+x) \underset{0}{\sim} x - \dfrac{1}{2}x^2 \,\,\,\, \Longrightarrow \,\,\,\, \ln^2(1+x) \underset{0}{\sim} \left( x - \dfrac{1}{2}x^2 \right)^2 \,\,\,\, \Longrightarrow \,\,\,\, \ln^2(1+x) = \left( x - \dfrac{1}{2}x^2 + o(x^2)\right)^2$$
$$\bullet \,\, (1-\cos(x)) \underset{0}{\sim} \dfrac{1}{2}x^2 \,\,\,\, \Longrightarrow \,\,\,\, (1-\cos(x)) = \dfrac{1}{2}x^2 + o(x^3)$$
Posons :
$$N(x) = \sin^3(x) \times \ln^2(1+x) \times (1-\cos(x)) \,\,\,\, \Longrightarrow \,\,\,\, f(x) = \dfrac{N(x)}{x^7}$$
Ainsi, on obtient :
$$N(x) = (x + o(x^2))^3 \times \left( x - \dfrac{1}{2}x^2 + o(x^2)\right)^2 \times \left( \dfrac{1}{2}x^2 + o(x^3) \right)$$
Soit :
$$N(x) = \dfrac{1}{2}x^5 \times \left( x - \dfrac{1}{2}x^2 \right)^2 + o(x^8)$$
Soit encore :
$$N(x) = \dfrac{1}{2}x^5 \times x^2\left( 1 - \dfrac{1}{2}x \right)^2 + o(x^8)$$
Donc :
$$N(x) = \dfrac{1}{2}x^7 \times \left( 1 - \dfrac{1}{2}x \right)^2 + o(x^8)$$
On obtient alors :
$$N(x) = \dfrac{1}{2}x^7 \times \left( 1 - x + \dfrac{1}{4}x^2 \right) + o(x^8)$$
Comme on se limite à l'ordre $$8$$, on trouve que :
$$N(x) = \dfrac{1}{2}x^7 - \dfrac{1}{2}x^8 + o(x^8)$$
De fait, on aboutit à :
$$f(x) = \dfrac{N(x)}{x^7} = \dfrac{\dfrac{1}{2}x^7 - \dfrac{1}{2}x^8 + o(x^8)}{x^7} = \dfrac{1}{2} - \dfrac{1}{2}x + o(x)$$
Finalement :
$${\color{red}{\boxed{\ell = \lim_{x \longrightarrow 0^+} f(x) = \dfrac{1}{2} }}}$$
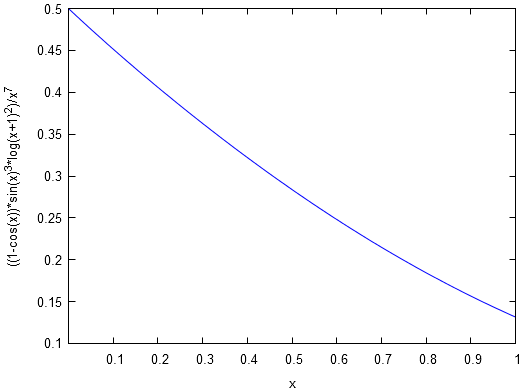
Graphiquement, on vérifie ceci sans difficulté :