La règle de l'Hôpital (cours)

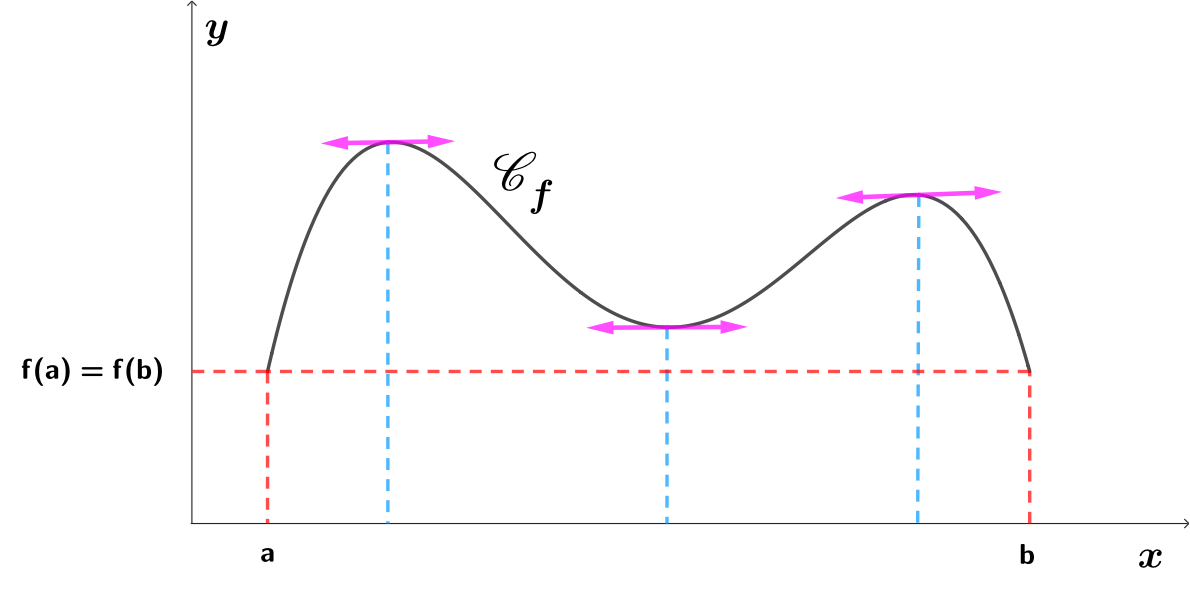
$${\color{red}{\looparrowright \,\, \textbf{Premier point : le théorème de Rolle}}}$$
Soit $$a$$ et $$b$$ deux nombres réels distincts tel que $$a<b$$. On considère une fonction $$f$$ continue sur l'intervalle $$[a\,;\,b]$$ mais dérivable sur $$]a\,;\,b[$$.
Le théorème de $$Rolle$$ nous apprend que si $$f(a) = f(b)$$ alors il existe au moins un nombre réel $$c$$ dans l'intervalle $$]a\,;\,b[$$ tel que $$f'(c) = 0$$, c'est-à-dire qu'en $$x=c$$ il y a existence d'une tangente horizontale.
Ce résultat se représente par :

Si la fonction $$f$$ est constante sur l'intervalle $$[a\,;\,b]$$ alors le résultat est direct car la représentation graphique de $$f$$ est une droite horizontale, et de fait il existe bien au moins un point d'abscisse $$x=c$$ qui admet une tangente horizontale, soit $$f'(c) = 0$$.
Si la fonction $$f$$ n'est pas constante alors de fait $$f$$ admet un maximum $$M$$ et un minimum $$m$$ sur l'intervalle $$[a\,;\,b]$$ considéré. De plus, il est évident qu'au moins l'une des deux valeurs, $$m$$ ou $$M$$ est différente de $$f(a)$$. Par exemple, supposons que $$M > f(a)$$. Supposons que $$M$$ se réalise à l'abscisse $$c$$ telle que $$a < c < b$$. Dans ce cas $$M = f(c)$$ et de fait $$f'(c) = 0$$. Ce qui achève la démonstration. Ce résultat est connu sous le nom de $${\color{red}{\textbf{théorème de Rolle}}}$$

$${\color{red}{\looparrowright \,\, \textbf{Deuxième point : le théorème de Cauchy}}}$$
Soit $$a$$ et $$b$$ deux nombres réels distincts tel que $$a<b$$. On considère maintenant deux fonctions $$f$$ et $$g$$ continues sur l'intervalle $$[a\,;\,b]$$ mais dérivables sur $$]a\,;\,b[$$. Dans ce cas, il existe un nombre réel $$c$$ appartenant à l'intervalle $$]a\,;\,b[$$ qui satisfait à l'égalité :
$$\dfrac{f(b) - f(a)}{g(b) - g(a)} = \dfrac{\dfrac{f(b) - f(a)}{b-a}}{\dfrac{g(b) - g(a)}{b-a}} = \dfrac{f'(c)}{g'(c)}$$
On construit maintenant la fonction $$\varphi$$ suivante :
$$\varphi : x \in [a\,;\,b] \longrightarrow \varphi(x) = f(x) - f(a) - \dfrac{f(b) - f(a)}{g(b) - g(a)} \left( g(x) - g(a) \right)$$
De par sa construction, cette fonction $$\varphi$$ est donc continue sur l'intervalle $$[a\,;\,b]$$ mais dérivable sur $$]a\,;\,b[$$. Sa dérivée est donnée par l'expression :
$$\varphi' : x \in ]a\,;\,b[ \longrightarrow \varphi'(x) = f'(x) - \dfrac{f(b) - f(a)}{g(b) - g(a)} g'(x)$$
De plus, on constate que :
$$\bullet \,\, \varphi(a) = f(a) - f(a) - \dfrac{f(b) - f(a)}{g(b) - g(a)} \left( g(a) - g(a) \right) = 0$$
$$\bullet\, \bullet \,\, \varphi(b) = f(b) - f(a) - \dfrac{f(b) - f(a)}{g(b) - g(a)} \left( g(b) - g(a) \right) = 0$$
On constate que la fonction $$\varphi$$ satisfait aux conditions d'application du théorème de $$Rolle$$. Ce théorème nous permet donc d'affirmer qu'il existe au moins un nombre réel $$c \in ]a\,;\,b[$$ tel que :
$$\varphi'(c) = 0$$
Ce qui nous donne donc :
$$f'(c) - \dfrac{f(b) - f(a)}{g(b) - g(a)} g'(c) = 0 \,\,\, \Longleftrightarrow \,\,\, f'(c) = \dfrac{f(b) - f(a)}{g(b) - g(a)} g'(c)$$
On en déduit donc que :
$$\dfrac{f(b) - f(a)}{g(b) - g(a)} = \dfrac{f'(c)}{g'(c)}$$
Ce qui achève la démonstration. Ce résultat est connu sous le nom de $${\color{red}{\textbf{théorème de Cauchy}}}$$.

$${\color{red}{\looparrowright \,\, \textbf{Troisième point : la règle de l'Hôpital}}}$$
Soit $$a$$, $$p$$ et $$b$$ trois nombres réels distincts tel que $$a<p<b$$. On considère maintenant deux fonctions $$f$$ et $$g$$ continues sur l'intervalle $$[a\,;\,b]$$ mais dérivables sur $$[a\,;\,b] \setminus \left\lbrace p \right\rbrace$$. En outre, on suppose que $$f(p) = g(p) = 0$$, et que $$\forall x \in [a\,;\,b] \setminus \left\lbrace p \right\rbrace$$, on a $$g'(x) \neq 0$$. De plus, pour $$x \neq p$$, on a $$g(x) \neq 0$$.
Sous ces hypothèses, le quotient $$\dfrac{f(x)}{g(x)}$$ existe bien pour $$x \neq p$$. Donc, on a alors :
$$\forall x \neq p, \,\,\ \dfrac{f(x)}{g(x)} = \dfrac{f(x) - 0}{g(x) - 0} = \dfrac{f(x) - f(p)}{g(x) - g(p)}$$
Dans ce cas, le résultat du $${\color{red}{\textbf{Deuxième point}}}$$ nous pouvons écrire qu'il existe un nombre réel $$c$$ qui appartient à l'intervalle $$]p\,;\,x[$$ tel que :
$$\dfrac{f(x) - f(p)}{g(x) - g(p)} = \dfrac{f'(c)}{g'(c)}$$
Et de fait, cela entraine que :
$$\dfrac{f(x)}{g(x)} = \dfrac{f'(c)}{g'(c)}$$
Passons maintenant à la limite lorsque $$x \, \longrightarrow \, p$$. On a, évidemment $$\lim_{x \, \longrightarrow \, p} c = p$$. De plus, selon nos hypothèses, la limite $$\lim_{x \, \longrightarrow \, p}\dfrac{f'(x)}{g'(x)}$$ existe, et on pose alors :
$$\lim_{x \, \longrightarrow \, p}\dfrac{f'(x)}{g'(x)} = \ell \in \mathbb{R}$$
Ainsi, on a le résultat suivant :
$${\color{red}{\boxed{\lim_{x \, \longrightarrow \, p}\dfrac{f'(x)}{g'(x)} = \ell \,\,\,\,\, \Longrightarrow \,\,\,\,\, \lim_{x \, \longrightarrow \, p}\dfrac{f(x)}{g(x)} = \ell }}}$$
Ce résultat est connu sous le nom de $${\color{red}{\textbf{règle de l'Hôpital}}}$$. Sous réserve de l'existence des dérivées $$f'$$ et $$g'$$ alors la limite du quotient de $$f$$ et $$g$$ est la même que celle du quotient de $$f'$$ et $$g'$$. On dit parfois que le quotient de deux fonction se comporte localement comme le quotient des dérivées associées.
Il faut bien prendre en compte que la $${\color{red}{\textbf{réciproque de la règle de l'Hôpital n'existe pas !}}}$$
La règle de L'Hospital quelle que soit sa forme peut être itérée. En effet, cette règle dit en substance, que pour calculer la limite d'un quotient on peut remplacer les fonctions par leurs dérivées. Mais à leur tour on peut remplacer ces dérivées par leurs propres dérivées, c'est à dire par les dérivées secondes des fonctions initiales, et ainsi de suite.

$${\color{blue}{\looparrowright \,\, \textbf{Remarque historique}}}$$
Cette règle apparaît pour la première fois en 1696 dans le traité Analyse des infiniment petits de Guillaume de L'Hospital, qui est le premier livre sur le calcul différentiel. Elle serait en fait due à Jean Bernoulli, qui l'aurait découverte deux ans plus tôt.

$${\color{blue}{\looparrowright \,\, \textbf{Exemple}}}$$
On a :
$$\lim_{x \, \longrightarrow \, 1}\dfrac{x-1}{x^2 + x - 2}$$
Les fonctions dérivées de $$x-1$$ et de $$x^2 + x - 2$$ existe bien sur $$\mathbb{R}$$. Puis, $$(x-1)' = 1$$ et $$(x^2 + x - 2)' = 2x + 1$$. De plus, on constate que $$(x^2 + x - 2)'_{x = 1} = 2\times 1 + 1 = 3 \neq 0$$. Donc, on peut écrire que :
$$\lim_{x \, \longrightarrow \, 1}\dfrac{(x-1)'}{(x^2 + x - 2)'} = \lim_{x \, \longrightarrow \, 1}\dfrac{1}{2x+1} = \dfrac{1}{3}$$
Ce qui implique, selon la règle de l'$$Hôspital$$, que :
$$\lim_{x \, \longrightarrow \, 1}\dfrac{x-1}{x^2 + x - 2} = \dfrac{1}{3}$$