Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Calculs de dérivées et de différentielles : Mise en pratique épisode 7 - Exercice 1
1 h
90
Les fonctions hyperboliques réciproques usuelles sont les suivantes :
la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction est non dérivable en car on il y a l'existence d'une tangente verticale. Son graphe représentatif est la suivant :
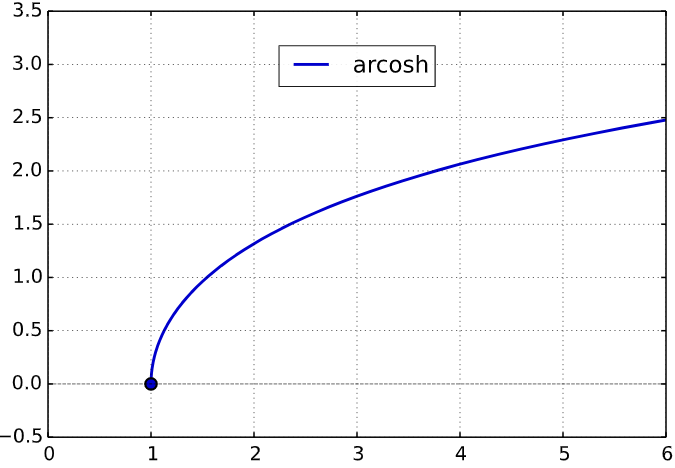
la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction est dérivable sur . Son graphe représentatif est la suivant :
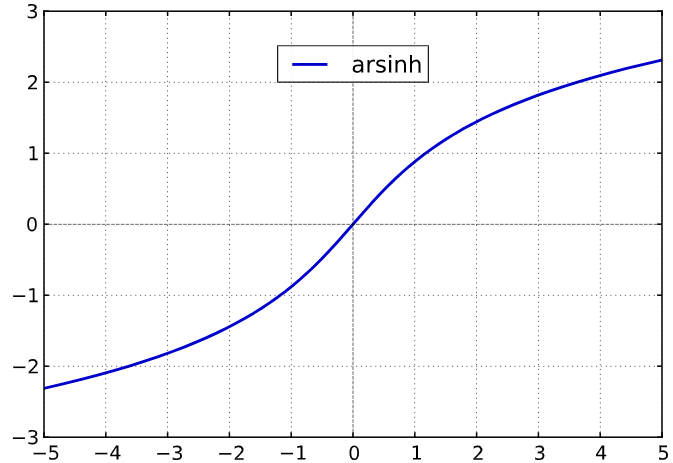
la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction n'est pas dérivable en . Son graphe représentatif est la suivant :
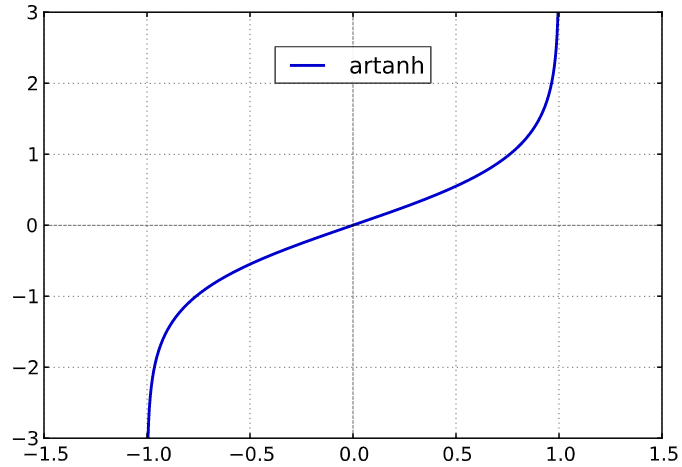
la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction n'est pas dérivable en . Son graphe représentatif est la suivant :
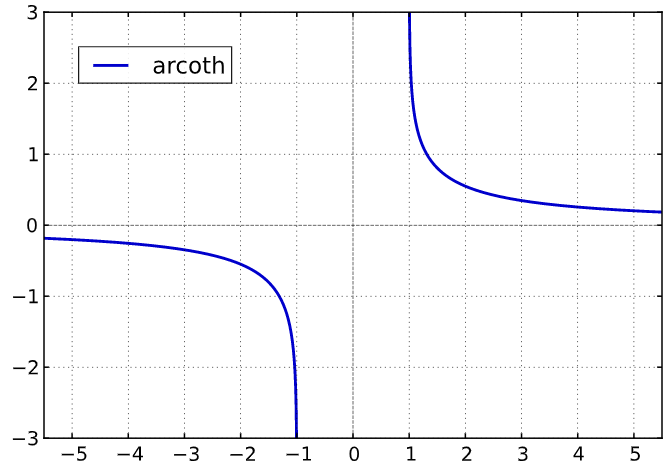 On remarquera également que :
On remarquera également que :
Pour chacune des fonctions suivantes, déterminer la fonction dérivée et la différentielle associée .
la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction est non dérivable en car on il y a l'existence d'une tangente verticale. Son graphe représentatif est la suivant :

la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction est dérivable sur . Son graphe représentatif est la suivant :

la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction n'est pas dérivable en . Son graphe représentatif est la suivant :

la fonction , notée , , ou . Puis, on a les propriétés suivantes :
Cette fonction n'est pas dérivable en . Son graphe représentatif est la suivant :

Pour chacune des fonctions suivantes, déterminer la fonction dérivée et la différentielle associée .
Question 1
Soit
Correction
On a :
Soit :
Soit encore :
Ce qui s'écrit aussi :
Or, , donc . On a alors :
Ainsi :
A savoir :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Soit :
Soit encore :
Ce qui s'écrit aussi :
Or, , donc . On a alors :
Ainsi :
A savoir :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Question 2
Soit
Correction
On a :
Soit :
Soit encore :
Ce qui nous donne :
Cependant, , ce qui implique que . Donc :
En simplifiant :
Soit encore :
On obtient alors :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Soit :
Soit encore :
Ce qui nous donne :
Cependant, , ce qui implique que . Donc :
En simplifiant :
Soit encore :
On obtient alors :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Question 3
Soit
Correction
On a :
Soit encore :
Ce qui nous donne :
En factorisant, on obtient :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Soit encore :
Ce qui nous donne :
En factorisant, on obtient :
Finalement :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Question 4
Soit
Correction
On a :
Soit :
Soit encore :
Ce qui nous donne :
Donc :
En tenant compte que, pour réel, on a , on obtient alors :
De même :
En simplifiant par sur , on trouve que :
D'où :
Finalement, on trouve que :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Soit :
Soit encore :
Ce qui nous donne :
Donc :
En tenant compte que, pour réel, on a , on obtient alors :
De même :
En simplifiant par sur , on trouve que :
D'où :
Finalement, on trouve que :
On a alors :
En faisant usage de l'écriture de , on peut donc écrire que :
Ainsi, la différentielle de est donnée par l'expression suivante :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.