Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Calculs de dérivées et de différentielles : Mise en pratique épisode 5 - Exercice 1

1 h
90
Les fonctions trigonométriques inverses, notées arcsin⁡\arcsin, arccos⁡\arccos et arctan⁡\arctan, sont également très importantes. Il faut donc s'entrainer avec elles également. On rappelle que :
∙  x∈]−1 ; 1[,   arccos⁡′(x)=−11−x2\bullet \,\, x \in ]-1\,;\,1[, \,\,\, \arccos'(x) = -\dfrac{1}{\sqrt{1-x^2}}
∙  x∈]−1 ; 1[,   arcsin⁡′(x)=11−x2\bullet \,\, x \in ]-1\,;\,1[, \,\,\, \arcsin'(x) = \dfrac{1}{\sqrt{1-x^2}}
∙  x∈R,   arctan⁡′(x)=11+x2\bullet \,\, x \in \mathbb{R}, \,\,\, \arctan'(x) = \dfrac{1}{1+x^2}
Il est également important de bien avoir "en tête" l'allure des graphes représentatifs de ces trois fonctions :
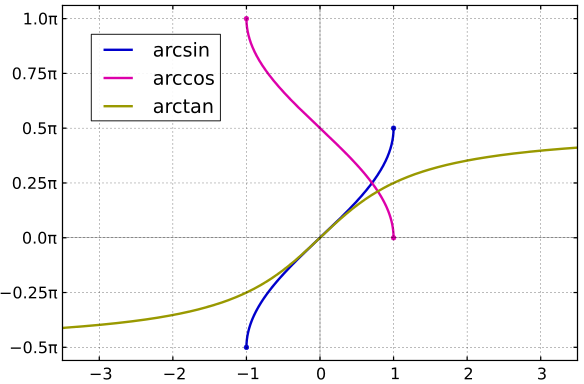Pour chacune des fonctions proposées, déterminer la fonction dérivée f′f' associée ainsi que la différentielle dfdf.
Question 1

Soit x∈R⟼f(x)=arccos⁡(1sin⁡(2x)−cos⁡(x))x \in \mathbb{R} \longmapsto f(x) = \arccos\left(\dfrac{1}{\sin(2x)-\cos(x)}\right)

Correction
On a :
f′(x)=(arccos⁡(1sin⁡(2x)−cos⁡(x)))′f'(x) = \left(\arccos\left(\dfrac{1}{\sin(2x)-\cos(x)}\right)\right)'
Ce qui nous donne :
f′(x)=(1sin⁡(2x)−cos⁡(x))′×−11−(1sin⁡(2x)−cos⁡(x))2f'(x) = \left(\dfrac{1}{\sin(2x)-\cos(x)}\right)' \times \dfrac{-1}{\sqrt{1-\left(\dfrac{1}{\sin(2x)-\cos(x)}\right)^2}}
Soit :
f′(x)=−−(sin⁡(2x)−cos⁡(x))′(sin⁡(2x)−cos⁡(x))2×11−1(sin⁡(2x)−cos⁡(x))2f'(x) = -\dfrac{-(\sin(2x)-\cos(x))'}{\left(\sin(2x)-\cos(x)\right)^2} \times \dfrac{1}{\sqrt{1-\dfrac{1}{\left(\sin(2x)-\cos(x)\right)^2}}}
Ainsi :
f′(x)=(sin⁡(2x)−cos⁡(x))′(sin⁡(2x)−cos⁡(x))2×11−1(sin⁡(2x)−cos⁡(x))2f'(x) = \dfrac{(\sin(2x)-\cos(x))'}{\left(\sin(2x)-\cos(x)\right)^2} \times \dfrac{1}{\sqrt{1-\dfrac{1}{\left(\sin(2x)-\cos(x)\right)^2}}}
Ce qui nous donne :
f′(x)=2cos⁡(2x)+sin⁡(x)(sin⁡(2x)−cos⁡(x))2×11−1(sin⁡(2x)−cos⁡(x))2f'(x) = \dfrac{2\cos(2x)+\sin(x)}{\left(\sin(2x)-\cos(x)\right)^2} \times \dfrac{1}{\sqrt{1-\dfrac{1}{\left(\sin(2x)-\cos(x)\right)^2}}}
Finalement, on obtient :
f′(x)=2cos⁡(2x)+sin⁡(x)(sin⁡(2x)−cos⁡(x))21−1(sin⁡(2x)−cos⁡(x))2{\color{red}{\boxed{f'(x) = \dfrac{2\cos(2x)+\sin(x)}{\left(\sin(2x)-\cos(x)\right)^2 \sqrt{1-\dfrac{1}{\left(\sin(2x)-\cos(x)\right)^2}}} }}}
On a alors :
f′(x)=dfdx(x)f'(x) = \dfrac{df}{dx}(x)
En faisant usage de l'écriture de LeibnizLeibniz, on peut donc écrire que :
df(x)=f′(x) dxdf(x) = f'(x) \, dx
Ainsi, la différentielle de ff est donnée par l'expression suivante :
df(x)=2cos⁡(2x)+sin⁡(x)(sin⁡(2x)−cos⁡(x))21−1(sin⁡(2x)−cos⁡(x))2 dx{\color{red}{\boxed{df(x) = \dfrac{2\cos(2x)+\sin(x)}{\left(\sin(2x)-\cos(x)\right)^2 \sqrt{1-\dfrac{1}{\left(\sin(2x)-\cos(x)\right)^2}}} \, dx}}}
Question 2

Soit x∈[5 ; 6]⟼f(x)=arcsin⁡(exsin⁡(x))x \in [5\,;\,6] \longmapsto f(x) = \arcsin\left(e^{x\sin(x)}\right)

Correction
On a :
f′(x)=(arcsin⁡(exsin⁡(x)))′=(exsin⁡(x))′11−(exsin⁡(x))2=(xsin⁡(x))′exsin⁡(x)11−(e2xsin⁡(x))f'(x) = \left(\arcsin\left(e^{x\sin(x)}\right) \right)' = \left(e^{x\sin(x)}\right)' \dfrac{1}{\sqrt{1-\left(e^{x\sin(x)}\right)^2}} = \left(x\sin(x)\right)' e^{x\sin(x)} \dfrac{1}{\sqrt{1-\left(e^{2x\sin(x)}\right)}}
Soit :
f′(x)=(sin⁡(x)+xcos⁡(x))exsin⁡(x)1−(e2xsin⁡(x))f'(x) = \left(\sin(x) + x\cos(x)\right) \dfrac{e^{x\sin(x)}}{\sqrt{1-\left(e^{2x\sin(x)}\right)}}
Finalement, on trouve que :
f′(x)=(sin⁡(x)+xcos⁡(x))exsin⁡(x)1−(e2xsin⁡(x)){\color{red}{\boxed{f'(x) = \dfrac{\left(\sin(x) + x\cos(x)\right) e^{x\sin(x)}}{\sqrt{1-\left(e^{2x\sin(x)}\right)}} }}}
On a alors :
f′(x)=dfdx(x)f'(x) = \dfrac{df}{dx}(x)
En faisant usage de l'écriture de LeibnizLeibniz, on peut donc écrire que :
df(x)=f′(x) dxdf(x) = f'(x) \, dx
Ainsi, la différentielle de ff est donnée par l'expression suivante :
df(x)=(sin⁡(x)+xcos⁡(x))exsin⁡(x)1−(e2xsin⁡(x)) dx{\color{red}{\boxed{df(x) = \dfrac{\left(\sin(x) + x\cos(x)\right) e^{x\sin(x)}}{\sqrt{1-\left(e^{2x\sin(x)}\right)}} \, dx}}}
Question 3

Soit x∈R⟼f(x)=arctan⁡(arctan⁡(x2))x \in \mathbb{R} \longmapsto f(x) = \arctan\left(\arctan(x^2)\right)

Correction
On a :
f′(x)=(arctan⁡(arctan⁡(x2)))′=(arctan⁡(x2))′×11+(arctan⁡(x2))2f'(x) = \left(\arctan\left(\arctan(x^2)\right)\right)' = \left(\arctan(x^2)\right)' \times \dfrac{1}{1+\left(\arctan(x^2)\right)^2}
Ce qui nous donne :
f′(x)=(x2)′1+(x2)2×11+(arctan⁡(x2))2f'(x) = \dfrac{\left(x^2\right)'}{1+\left(x^2\right)^2} \times \dfrac{1}{1+\left(\arctan(x^2)\right)^2}
Soit :
f′(x)=2x1+(x2)2×11+(arctan⁡(x2))2f'(x) = \dfrac{2x}{1+\left(x^2\right)^2} \times \dfrac{1}{1+\left(\arctan(x^2)\right)^2}
Finalement :
f′(x)=2x(1+x4)(1+arctan⁡2(x2)){\color{red}{\boxed{f'(x) = \dfrac{2x}{\left( 1+x^4 \right)\left(1+\arctan^2(x^2)\right)} }}}
On a alors :
f′(x)=dfdx(x)f'(x) = \dfrac{df}{dx}(x)
En faisant usage de l'écriture de LeibnizLeibniz, on peut donc écrire que :
df(x)=f′(x) dxdf(x) = f'(x) \, dx
Ainsi, la différentielle de ff est donnée par l'expression suivante :
df(x)=2x(1+x4)(1+arctan⁡2(x2)) dx{\color{red}{\boxed{df(x) = \dfrac{2x}{\left( 1+x^4 \right)\left(1+\arctan^2(x^2)\right)} \, dx}}}
Question 4

Soit x∈]0 ; 0,9]⟼f(x)=arctan⁡(arcsin⁡(arccos⁡(11+x2)))x \in ]0\,;\,0,9] \longmapsto f(x) = \arctan\left(\arcsin\left(\arccos\left( \dfrac{1}{1+x^2} \right)\right)\right)

Correction