Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
A la limite du supportable ! - Exercice 1
1 h
90
Un exercice de détermination des limites.
Question 1
Déterminer les limites suivantes.
Correction
La limite proposée est une forme indéterminée du type .
La fonction du numérateur est dérivable, donc continue, sur . Il en est de même pour la fonction du dénominateur . En outre cette dernière fonction ne s'annule jamais sur . De plus, on a :
Donc, la limite est encore une forme indéterminée du type . Nous allons donc réitérer la procédure. On a alors :
La fonction dérivée seconde s'annulle vers , et est donc positive au voisinage très proche de lorsque .
On en déduit donc que :
De fait, on peut finalement écrire que :
La fonction du numérateur est dérivable, donc continue, sur . Il en est de même pour la fonction du dénominateur . En outre cette dernière fonction ne s'annule jamais sur . De plus, on a :
Donc, la limite est encore une forme indéterminée du type . Nous allons donc réitérer la procédure. On a alors :
La fonction dérivée seconde s'annulle vers , et est donc positive au voisinage très proche de lorsque .
On en déduit donc que :
De fait, on peut finalement écrire que :
Question 2
Correction
On constate que cette limite se présente sous la forme d'une forme indéterminée du type .
Puis, sur l'intervalle la fonction se trouvant au numérateur est dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite est également une forme indéterminée du type . On va donc réitérer la procédure.
Sur l'intervalle la fonction se trouvant au numérateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite est à nouveau une forme indéterminée du type . On va donc réitérer une nouvelle fois la procédure.
Sur l'intervalle la fonction se trouvant au numérateur est trois fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite existe bien. Et on a :
On en déduit alors que :
Puis :
Et donc :
Finalement :
Dans ce cas précis, pour la fonction un prolongement par continuité est possible à l'origine en imposant la condition . Graphiquement, sur l'intervalle , on vérifie ceci avec la représentation graphique de :
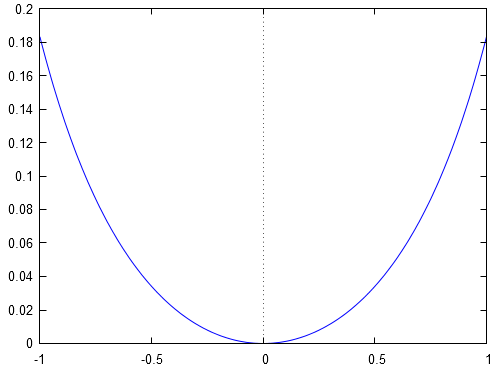
Puis, sur l'intervalle la fonction se trouvant au numérateur est dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite est également une forme indéterminée du type . On va donc réitérer la procédure.
Sur l'intervalle la fonction se trouvant au numérateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite est à nouveau une forme indéterminée du type . On va donc réitérer une nouvelle fois la procédure.
Sur l'intervalle la fonction se trouvant au numérateur est trois fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Puis, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue, et comme on a :
Ce qui implique que :
Et on constate alors que la limite existe bien. Et on a :
On en déduit alors que :
Puis :
Et donc :
Finalement :
Dans ce cas précis, pour la fonction un prolongement par continuité est possible à l'origine en imposant la condition . Graphiquement, sur l'intervalle , on vérifie ceci avec la représentation graphique de :

Question 3
avec et qui sont deux nombres réels strictement positifs.
Correction
La fonction est dérivable, donc continue sur . Il en est de même pour la fonction identité . Puis, on a :
Donc :
Finalement :
Donc :
Finalement :
Question 4
avec et qui sont deux nombres réels strictement positifs.
Correction
On constate que cette limite se présente sous la forme d'une forme indéterminée du type .
Puis, sur l'intervalle , la fonction se trouvant au numérateur est dérivable, donc continue. Donc, sur l'intervalle , on a:
Ce qui implique que :
De même, sur l'intervalle , la fonction se trouvant au dénominateur est dérivable, donc continue. Donc, sur l'intervalle , on a:
Ce qui implique que :
Ainsi, sur l'intervalle (et y appartient), la limite n'est pas définie car toujours du type . On réitère donc la procédure.
Sur l'intervalle , la fonction se trouvant au numérateur est deux fois dérivable, donc continue. Donc, sur l'intervalle , on a :
Ce qui implique que :
De même, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue. Donc, sur l'intervalle , on a :
Ce qui implique que :
Ainsi, sur l'intervalle (et y appartient), la limite existe. On a donc :
On en déduit donc que :
Finalement :
Puis, sur l'intervalle , la fonction se trouvant au numérateur est dérivable, donc continue. Donc, sur l'intervalle , on a:
Ce qui implique que :
De même, sur l'intervalle , la fonction se trouvant au dénominateur est dérivable, donc continue. Donc, sur l'intervalle , on a:
Ce qui implique que :
Ainsi, sur l'intervalle (et y appartient), la limite n'est pas définie car toujours du type . On réitère donc la procédure.
Sur l'intervalle , la fonction se trouvant au numérateur est deux fois dérivable, donc continue. Donc, sur l'intervalle , on a :
Ce qui implique que :
De même, sur l'intervalle , la fonction se trouvant au dénominateur est deux fois dérivable, donc continue. Donc, sur l'intervalle , on a :
Ce qui implique que :
Ainsi, sur l'intervalle (et y appartient), la limite existe. On a donc :
On en déduit donc que :
Finalement :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.