Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
- Tous les niveaux>
- Fonctions usuelles>
- Fonctions affines. Tableaux de signes . Inéquations produit et Inéquations quotient
Comment dresser le tableau de signe d'une fonction affine - Exercice 2
20 min
30
Question 1
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .

Question 2
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .

Question 3
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
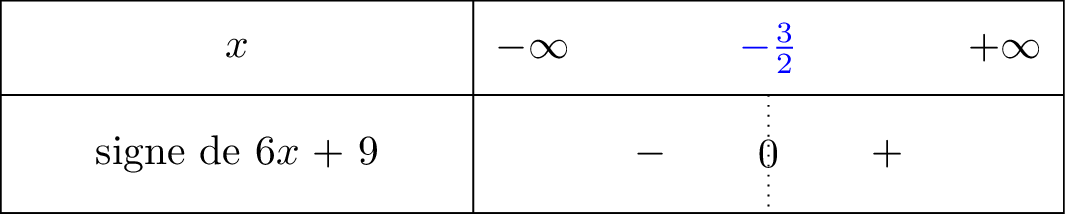 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .

Question 4
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .

Question 5
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine décroissante car son coefficient directeur . (Cela signifie que la fonction DESCEND donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .

Question 6
Dresser le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .
