Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Etude de fonctions - Exercice 5
30 min
50
Soit la fonction définie sur par où et étant deux constantes réelles.
Question 1
La courbe représentative de la fonction est donnée ci-dessous.
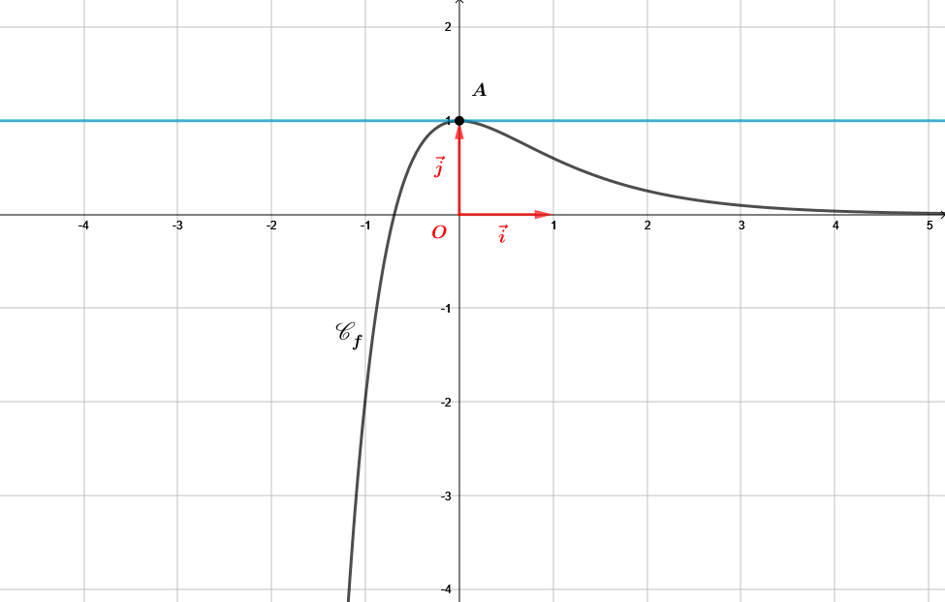 Cette courbe passe par le point et la tangente à en est parallèle à l’axe des abscisses. On note la fonction dérivée de .
Cette courbe passe par le point et la tangente à en est parallèle à l’axe des abscisses. On note la fonction dérivée de .

Donner les valeurs exactes de et .
Correction
D'après l'énoncé, la courbe passe par le point ce qui donne .
La tangente à en est parallèle à l’axe des abscisses. Or le coefficient directeur d'une tangente horizontale est nulle. Par définition, correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .
Ainsi
La tangente à en est parallèle à l’axe des abscisses. Or le coefficient directeur d'une tangente horizontale est nulle. Par définition, correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .
Ainsi
.
Question 2
Calculer .
Correction
est dérivable sur .
Ainsi : .
Ainsi :
Question 3
En déduire les valeurs de et .
Correction
D'après les questions précédentes, nous savons que : et .
équivaut successivement à :
équivaut successivement à :
Finalement, il nous faut résoudre le système suivant :
Il en résulte donc que :
Finalement, il nous faut résoudre le système suivant :
Il en résulte donc que :
Question 4
Montrer que , pour tout réel , on a :
Correction
est dérivable sur .
Maintenant, nous allons développer l'expression .
équivaut successivement à :
Maintenant, nous allons développer l'expression .
équivaut successivement à :
Question 5
Etudier le signe de et en déduire les variations de sur .
Correction
Pour tout réel ; on vérifie aisément que . Donc le signe de dépend alors de .
Il en résulte donc que :
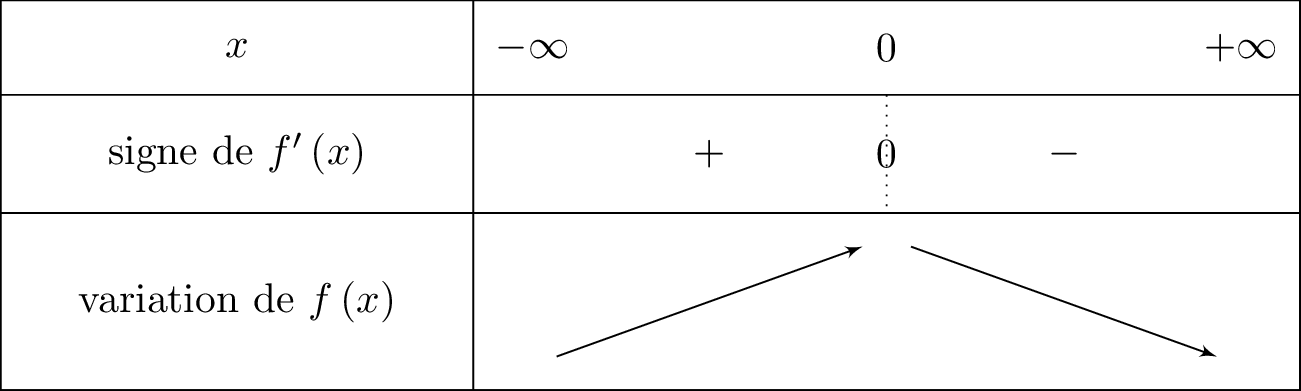
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.