Comment étudier les variations d'une fonction de la forme $$f\left(x\right)=ax^3+bx^2+cx+d$$ - Exercice 1

$$f$$ est dérivable sur $$\mathbb{R}$$.
$$f'\left(x\right)=3x^{2} -3$$
Ici la dérivée est une fonction du $$2$$^ème degré.
Pour l'étude du signe de $$3x^{2} -3$$, on va utiliser le discriminant.
Alors $$a=3$$; $$b=0$$ et $$c=-3$$.
Or $$\Delta =b^{2} -4ac$$ donc $$\Delta =36$$.
Il existe donc deux racines réelles distinctes.

• $$x_{1} =\frac{-b-\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{1} =-1$$.
• $$x_{2} =\frac{-b+\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{2} =1$$.

Comme $$a=3>0$$, la parabole est tournée vers le haut c'est-à-dire que $$f$$ est du signe de $$a$$ à l'extérieur des racines et du signe opposé à $$a$$ entre les racines.
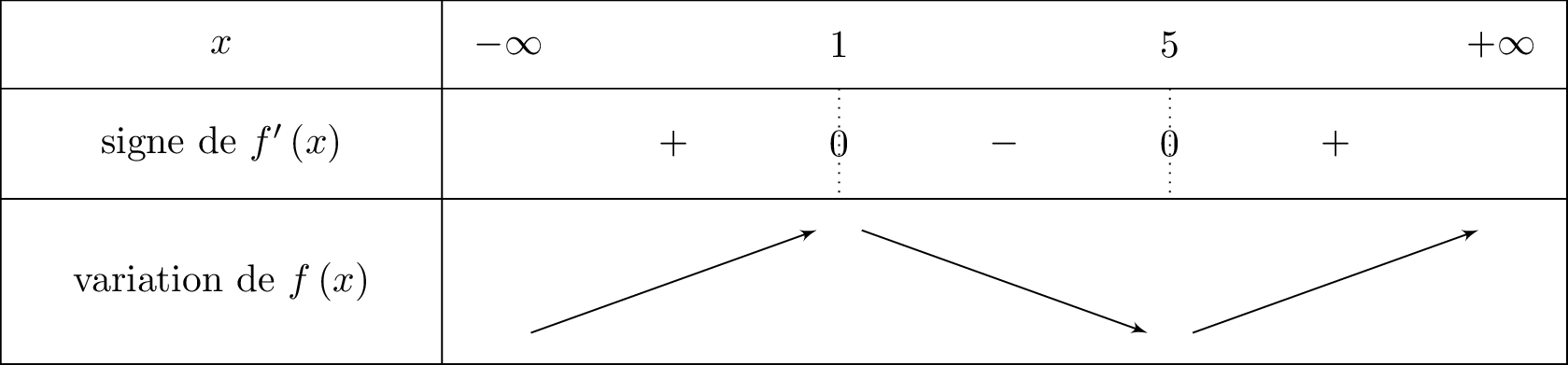
On en déduit le tableau de variation suivant :
On a :
$$f\left(-1\right)=\left(-1\right)^{3} -3\times\left(-1\right)-5=-3$$
$$f\left(1\right)=1^{3} -3\times1-5=-7$$

$$f$$ est dérivable sur $$\mathbb{R}$$.
$$f'\left(x\right)=\frac{1}{3} \times 3x^{2} -3\times 2x+5$$
$$f'\left(x\right)=x^{2} -6x+5$$
Ici la dérivée est une fonction du $$2$$^ème degré.
Pour l'étude du signe de $$x^{2} -6x+5$$, on va utiliser le discriminant.
Alors $$a=1$$; $$b=-6$$ et $$c=5$$.
Or $$\Delta =b^{2} -4ac$$ donc $$\Delta =16$$.
Il existe donc deux racines réelles distinctes.

• $$x_{1} =\frac{-b-\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{1} =1$$.
• $$x_{2} =\frac{-b+\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{2} =5$$.

Comme $$a=1>0$$, la parabole est tournée vers le haut c'est-à-dire que $$f'$$ est du signe de $$a$$ à l'extérieur des racines et du signe opposé à $$a$$ entre les racines.
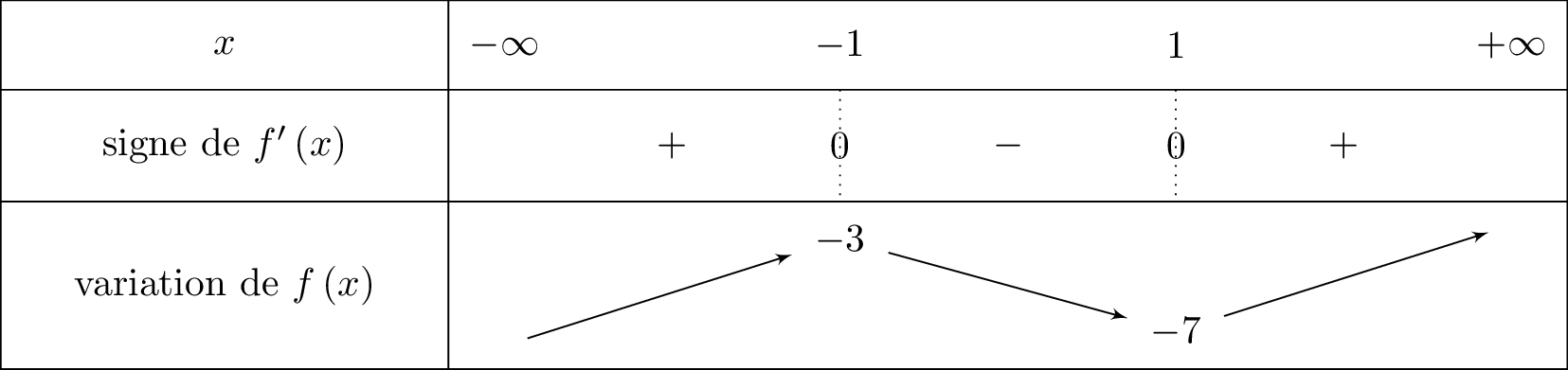
On en déduit le tableau de variation suivant :