Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Reconnaitre le signe de aa , cc et Δ\Delta à l'aide d'un graphique - Exercice 1

12 min
25
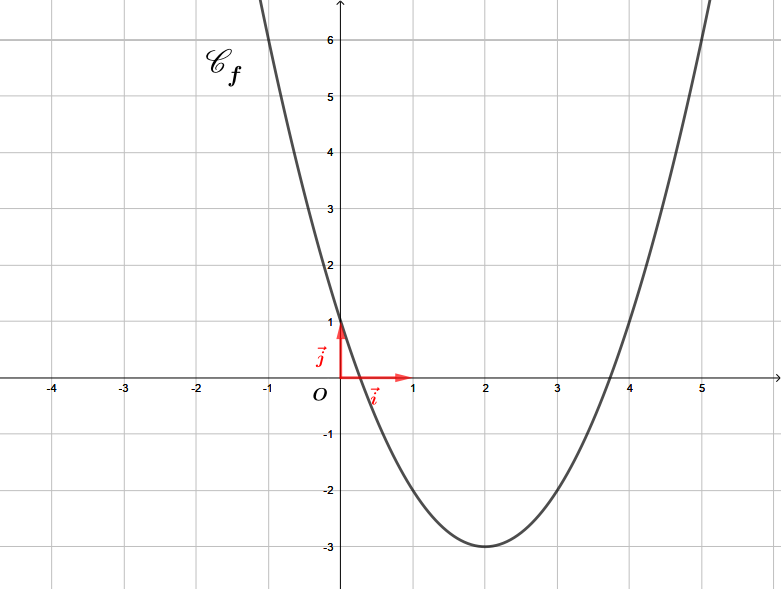
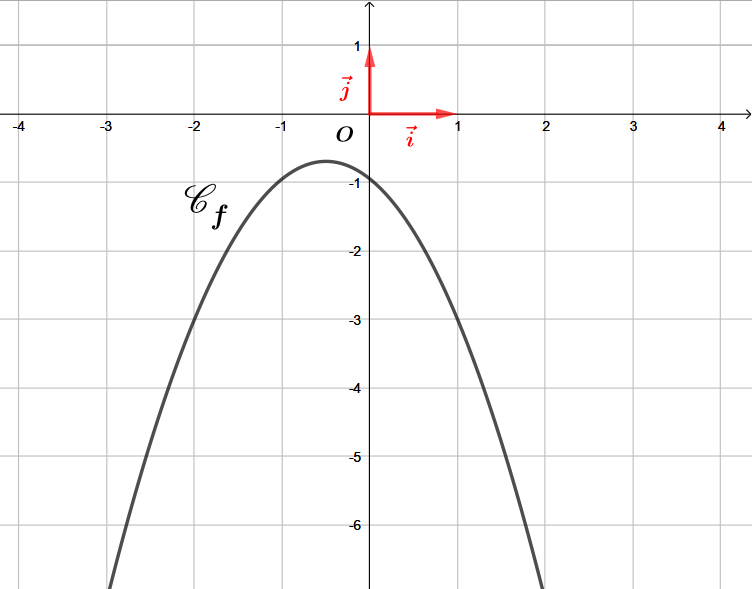
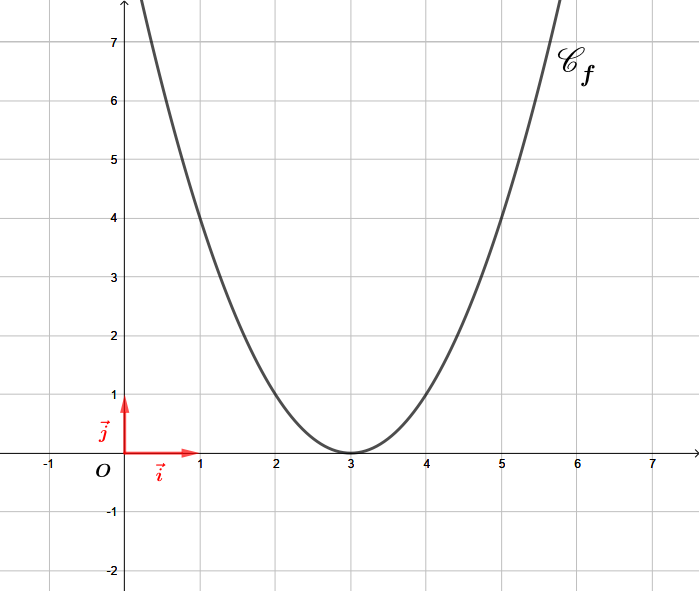
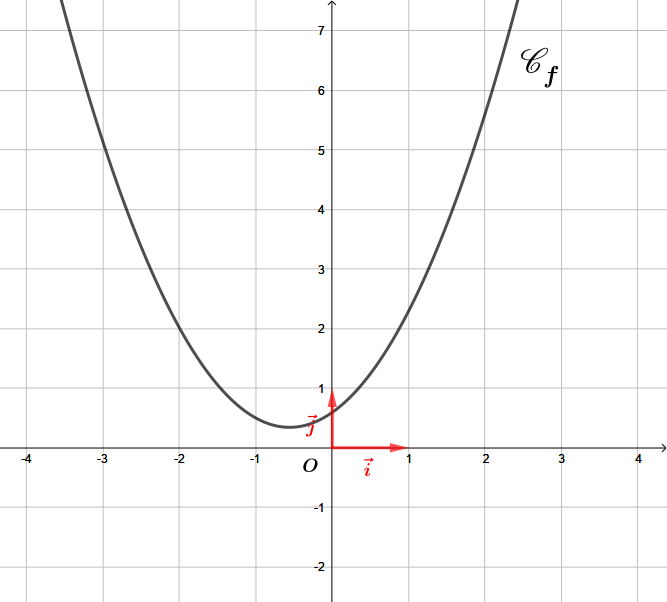
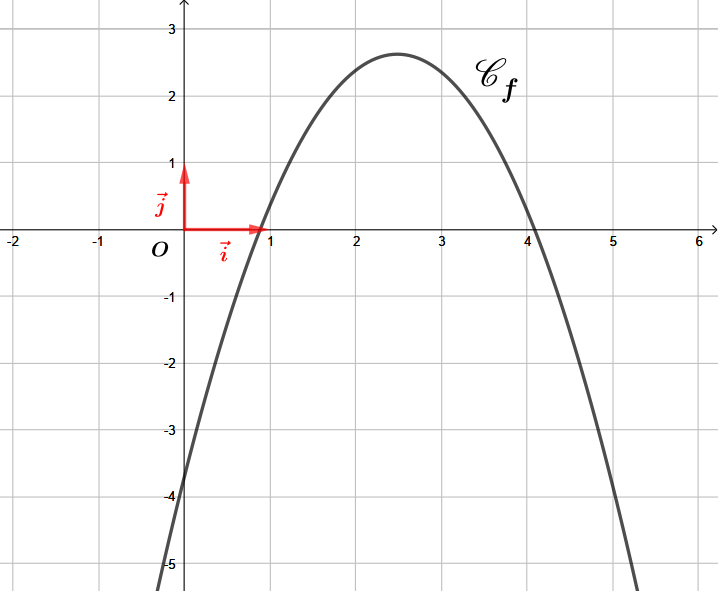
On a représenté ci-dessous plusieurs fonctions trinômes du second degré, de la forme f(x)=ax2+bx+cf\left(x\right)=ax^{2}+bx+c avec a≠0a\ne0 et bb et cc des réels.
Pour chacune des fonctions, indiquer le signe de aa , le signe de cc et enfin le signe de Δ\Delta.
Question 1

Correction
  • La parabole est tournée vers le haut , ce qui signifie que :
    a>0a>0
  • La parabole passe par deux fois par l'axe des abscisses. Ce qui signifie que l'équation f(x)=0f\left(x\right)=0 admet deux racines réelles distinctes. Il en résulte donc que :
    Δ>0\Delta>0
  • Pour déterminer le signe de cc, il nous suffit de déterminer le signe de l'image de 00 par ff. On lit facilement ici que f(0)≈1>0f\left(0\right)\approx1>0. Il en résulte donc que :
    c>0c>0
    • Question 2

    Correction
  • La parabole est tournée vers le bas , ce qui signifie que :
    a<0a<0
  • La parabole ne passe pas par l'axe des abscisses. Ce qui signifie que l'équation f(x)=0f\left(x\right)=0 n'admet pas de racines réelles. Il en résulte donc que :
    Δ<0\Delta<0
  • Pour déterminer le signe de cc, il nous suffit de déterminer le signe de l'image de 00 par ff. On lit facilement ici que f(0)≈−1<0f\left(0\right)\approx-1<0. Il en résulte donc que :
    c<0c<0
    • Question 3

    Correction
  • La parabole est tournée vers le haut , ce qui signifie que :
    a>0a>0
  • La parabole est tangent avec l'axe des abscisses, c'est à dire qu'elle ne passe une seule fois par l'axe des abscisses. Ce qui signifie que l'équation f(x)=0f\left(x\right)=0 admet une racine réelle. Il en résulte donc que :
    Δ=0\Delta=0
  • Pour déterminer le signe de cc, il nous suffit de déterminer le signe de l'image de 00 par ff. On lit facilement ici que f(0)>0f\left(0\right)>0. Il en résulte donc que :
    c>0c>0
    • Question 4

    Correction
  • La parabole est tournée vers le haut , ce qui signifie que :
    a>0a>0
  • La parabole ne passe pas par l'axe des abscisses. Ce qui signifie que l'équation f(x)=0f\left(x\right)=0 n'admet pas de racines réelles. Il en résulte donc que :
    Δ<0\Delta<0
  • Pour déterminer le signe de cc, il nous suffit de déterminer le signe de l'image de 00 par ff. On lit facilement ici que f(0)≈0,5>0f\left(0\right)\approx0,5>0. Il en résulte donc que :
    c>0c>0
    • Question 5

    Correction
  • La parabole est tournée vers le bas , ce qui signifie que :
    a<0a<0
  • La parabole passe par deux fois par l'axe des abscisses. Ce qui signifie que l'équation f(x)=0f\left(x\right)=0 admet deux racines réelles distinctes. Il en résulte donc que :
    Δ>0\Delta>0
  • Pour déterminer le signe de cc, il nous suffit de déterminer le signe de l'image de 00 par ff. On lit facilement ici que f(0)≈−3,8<0f\left(0\right)\approx-3,8<0. Il en résulte donc que :
    c<0c<0