Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types - Exercice 2
10 min
20
Comparer les fractions ci-dessous :
Question 1
et
Correction
- Pour comparer deux fractions de mêmes dénominateurs, il suffit de comparer les numérateurs.
- La fraction la plus grande sera la fraction ayant le plus grand numérateur.
- La fraction la plus petite sera la fraction ayant le plus petit numérateur.
on en déduit donc que :
Question 2
Comparer les fractions ci-dessous :
et
Correction
- Pour comparer deux fractions de dénominateurs différents il suffit de les mettre aux mêmes numérateurs. et de comparer les numérateurs.
- La fraction la plus grande sera la fraction ayant le plus grand numérateur.
- La fraction la plus petite sera la fraction ayant le plus petit numérateur.
Les fractions sont aux mêmes dénominateurs, on peut donc comparer les numérateurs.
on en déduit donc que :
Question 3
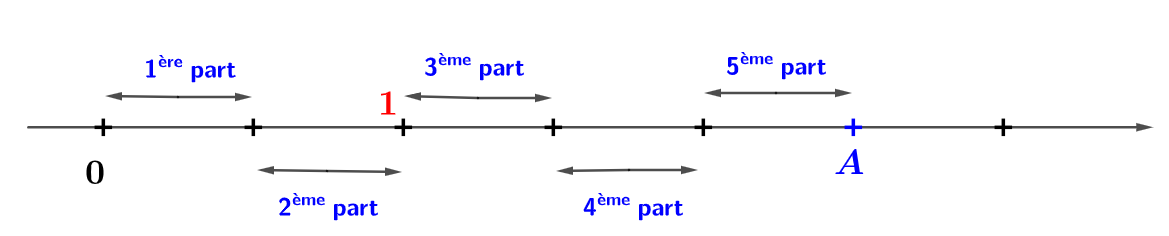
On considère la droite graduée ci-dessous : 

Lire l'abscisse des points et .
Correction
- Pour déterminer l'abscisse d'une fraction de la forme Avec , on procède de la manière suivante :
- Le numérateur correspond aux nombres de parts identiques pour arriver au point voulu en partant de .
- Le dénominateur correspond toujours aux nombres de parts identiques qui sépare l'unité.
L'abscisse du point est donc
Question 4
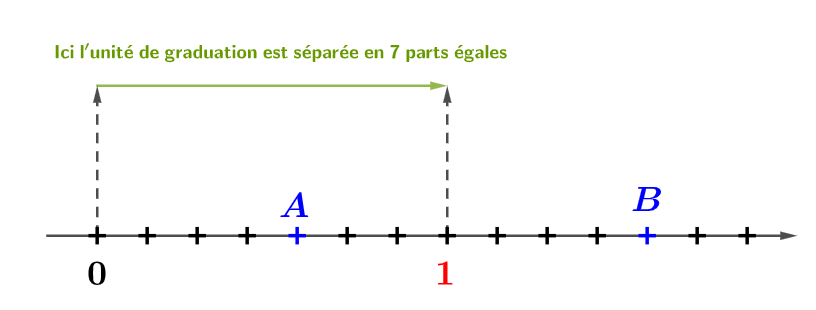
Placer sur une droite graduée le point d'abscisse
Correction
- Pour placer l'abscisse d'une fraction de la forme Avec , on procède de la manière suivante :
- On découpe toujours l'unité (entre et ) en part égale correspondant à , le dénominateur.
Ensuite, en partant de on se déplace de parts égales correspond à le numérateur. Ici se trouve l'abscisse du point.
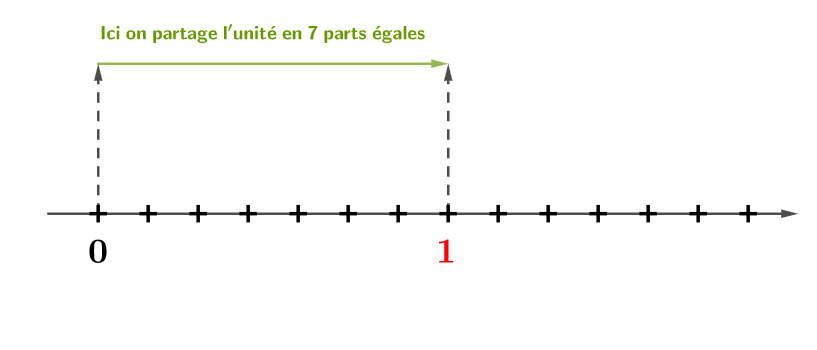
On doit d'abord partager l'unité en parts égales.
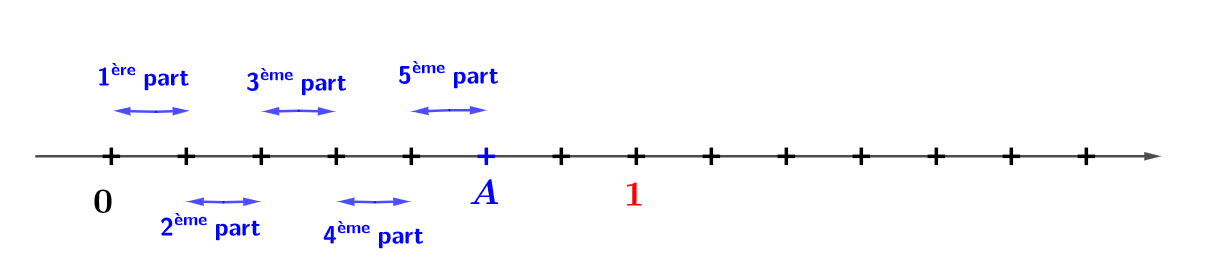
Ici se trouve l'abscisse du point .
Question 5
Placer sur une droite graduée le point d'abscisse
Correction
- Pour placer l'abscisse d'une fraction de la forme Avec , on procède de la manière suivante :
- On découpe toujours l'unité (entre et ) en part égale correspondant à , le dénominateur.
Ensuite, en partant de on se déplace de parts égales correspond à le numérateur. Ici se trouve l'abscisse du point.
On doit d'abord partager l'unité en parts égales.
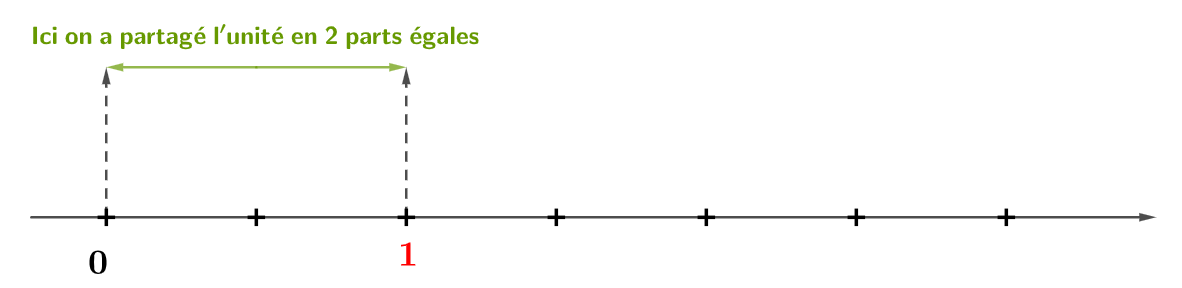
Ici se trouve l'abscisse du point .