Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 1ère partie - Exercice 1

5 min
10
Question 1
On considère le quadrilatère ABCDABCD ci-dessous :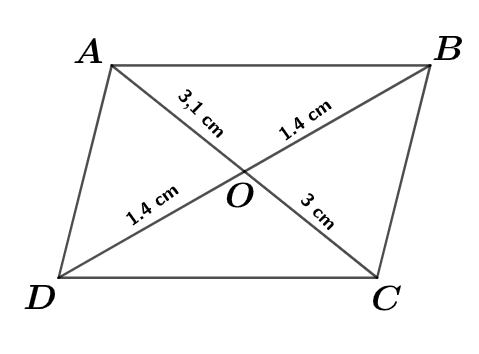

Le quadrilatère ABCDABCD est-il un parallélogramme ??

Correction
    Voici les propriétés qui permettent de démontrer qu'un quadrilatère est un parallélogramme :

    ∙    \bullet\;\;Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
    ∙    \bullet\;\;Un quadrilatère qui a ses côtés opposés 2\color{red}2 à 2\color{red}2 de mêmes longueurs est un parallélogramme.
    ∙    \bullet\;\;Un quadrilatère qui a ses côtés opposés parallèles 2\color{red}2 à 2\color{red}2 est un parallélogramme.
    ∙    \bullet\;\;Un quadrilatère qui a ses angles opposés de mêmes mesures est un parallélogramme.
Dans le quadrilatère ABCDABCD, on a OD=OBOD=OB mais OA≠OC.OA\neq OC.
Les diagonales du quadrilatère ABCDABCD ne se coupent pas en leur milieu .

On peut donc conclure que le quadrilatère ABCDABCD n'est pas un parallélogramme.
Question 2

Que faudrait-il changer au minimum au quadrilatère ABCDABCD pour que celui-ci soit un parallélogramme.

Correction
    ∙    \bullet\;\;Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
Dans le quadrilatère ABCDABCD il faudrait que les diagonales ACAC et BDBD se coupent en leur milieu pour que le quadrilatère ABCDABCD soit un parallélogramme.
On doit donc avoir DO=OBDO=OB (Qui est déjà le cas) et AO=OCAO=OC (qui n'est pas encore le cas).
On devrait alors modifier la longueur du segment AOAO ou OCOC pour que ABCDABCD soit un parallélogramme.
Il nous faudrait avoir : AO=OC=3  cm  ou  AO=OC=3,1  cm\boxed{AO=OC=3\;cm\;ou\;AO=OC=3,1\;cm}

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.