Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Somme des angles dans un triangle particulier - Exercice 3

5 min
15
On considère le triangle FGHFGH isocèle en HH ci-dessous :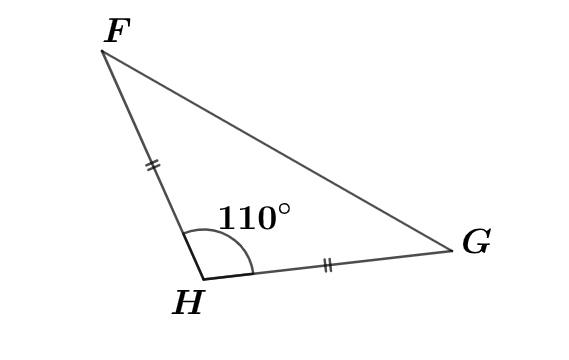
Question 1

Calculer la mesure de l'angle F^\widehat{F} et de l'angle G^\widehat{G}.

Correction
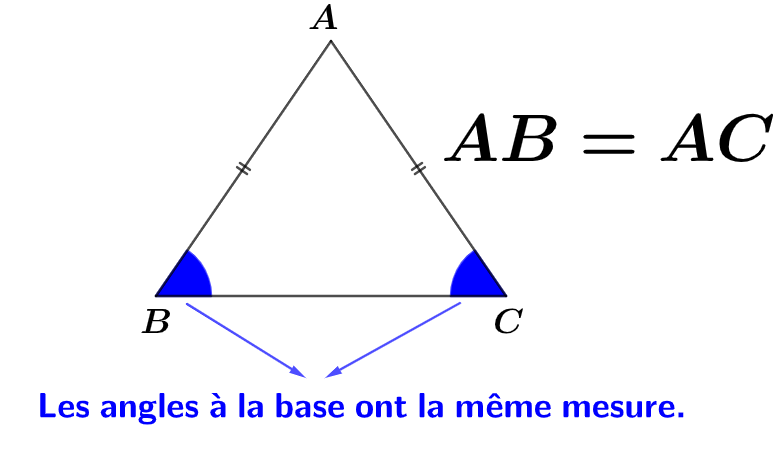
  • Un triangle isocèle, est un triangle qui a deux côtés de la même longueur.
  • Les angles à la base d'un triangle isocèle sont de la même mesure.
Le triangle FGHFGH est isocèle en HH donc les angles à la base ont la même mesure.
On a donc : F^=G^\widehat{F}=\widehat{G}
  • Dans un triangle, la somme des trois angles est égale à 180°.\color{red}180\degree.
F^+G^+H^=180°\widehat{F}+\widehat{G}+\widehat{H}=180\degree
L'angle H^\widehat{H} mesure 110°110\degree, on a donc :
F^+G^+110=180°\widehat{F}+\widehat{G}+110=180\degree
F^+G^=180−110=70°\widehat{F}+\widehat{G}=180-110=70\degree
Puisque les angles F^\widehat{F} et G^\widehat{G} sont de la même mesure, il suffit de diviser le résultat par 2\color{red}2 pour avoir la mesure de chacun des deux angles.
F^=G^=702=35°\widehat{F}=\widehat{G}=\frac{70}{2}=35\degree
Les angles F^\color{blue}{\widehat{F}} et G^\color{blue}{\widehat{G}} mesurent 35°\color{blue}35\degree.