Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 3
8 min
20
On considère un triangle rectangle en tel que l'angle .
Question 1
Calculer la mesure de l'angle .
Correction
Dans un premier temps, on peut réaliser un croquis de notre triangle.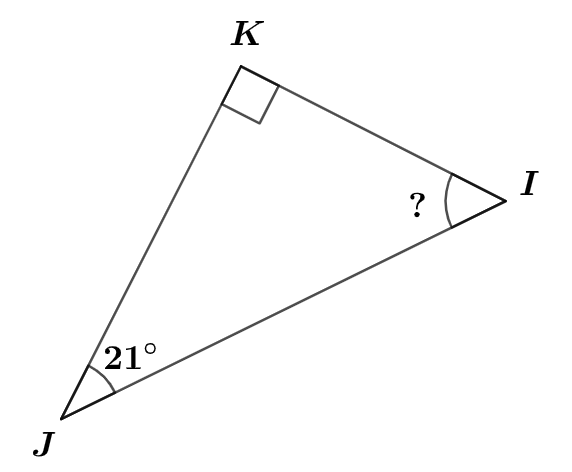
Méthode 1 :Dans le triangle on connait la mesure de angles, l'angle et l'angle .
On a donc :
Or dans un triangle, la somme des trois angles est égale à
On peut donc calculer la mesure du troisième angle :
L'angle mesure .
Méthode 2 :Dans le triangle rectangle , les deux angles aigus sont l'angle et l'angle .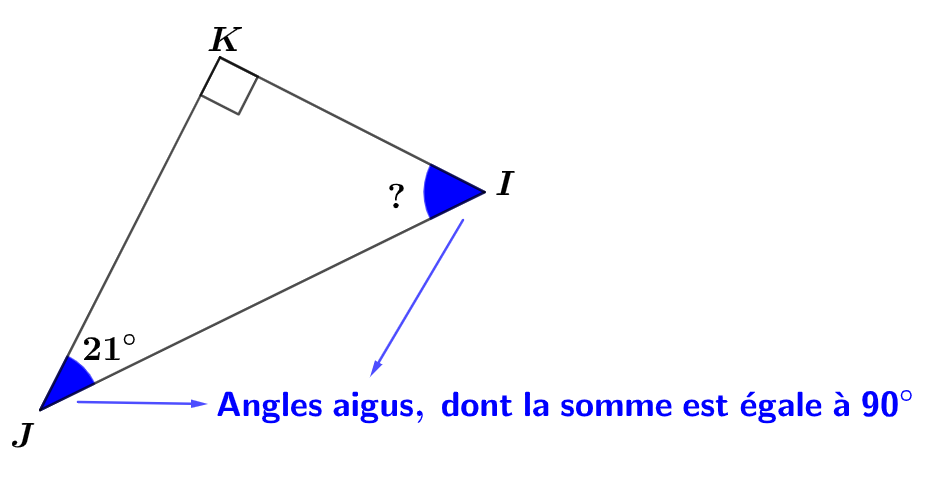 Donc :
Donc :
L'angle mesure .

Méthode 1 :
- Dans un triangle, la somme des trois angles est égale à
On a donc :
Or dans un triangle, la somme des trois angles est égale à
On peut donc calculer la mesure du troisième angle :
L'angle mesure .
Méthode 2 :
- Dans un triangle rectangle, la somme des deux angles aigus est égale à

L'angle mesure .
Question 2
On considère un triangle tel que :
Démontrer que le triangle est un triangle rectangle.
Correction
- Un triangle rectangle est un triangle qui possède un angle droit, c'est-à-dire un angle de .
Donc pour le moment nous n'avons pas d'angle de .
Calculons la mesure de l'angle :
- Dans un triangle, la somme des trois angles est égale à
On a donc :
Or dans un triangle, la somme des trois angles est égale à
On peut donc calculer la mesure du troisième angle :
L'angle mesure .
On peut donc conclure que le triangle est bien un triangle rectangle.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.