Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Savoir utiliser et reconnaitre les hauteurs d'un triangle et médiatrices d'un segment - Exercice 5

8 min
15
Question 1
On considère un triangle ABCABC quelconque.

Tracer les trois hauteurs du triangle ABCABC.

Correction
  • Définition d'une hauteur :
    Dans un triangle, la hauteur issue d'un sommet, est la droite qui passe par ce sommet et qui coupe le côté opposé perpendiculairement.
Protocole de construction de la hauteur issue de A :
  • Puisque la hauteur est issue de A, alors elle devra passer par le point A.
    ⁣Ensuite, on pose un côté de l'angle droit de l'équerre ou de la réquerre sur le côté opposé au point A, dans notre cas le segment [BC].[BC].
  • On fait glisser l'équerre ou la réquerre sur le segment [BC][BC] jusqu'à arriver au point A.
  • Ensuite, on peut tracer la hauteur issue de A. (Ici la droite en bleu).
    On reproduit après le même protocole partant des points B\color{red}B et C\color{red}C.
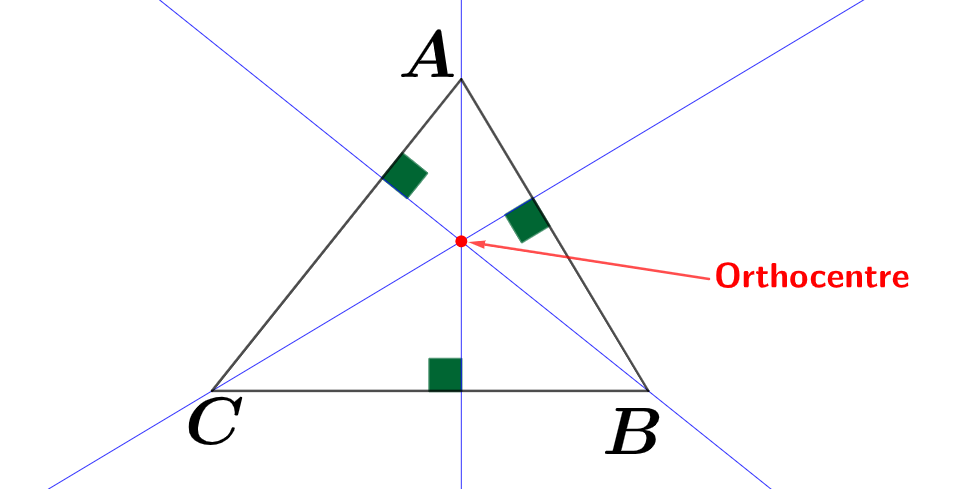
    Voici un triangle avec ses trois hauteurs :
    • Question 2

    Que peut-on dire des trois hauteurs du triangle obtenu à la question précédente ??

    Correction
    • Les 33 hauteurs d'un triangle se coupent en un point. On appelle ce point l'orthocentre.
    Les 33 hauteurs d'un triangle se coupent en un point, on l'observe sur notre figure.
    Important : lorsque l'on trace les 33 hauteurs d'un triangle, si elles ne se coupent pas en un seul point, alors il y a une erreur sur le tracé d'une ou plusieurs hauteurs.