🔴  Lives #BAC2024

À partir du 12 mai, révise le bac avec nous sur YouTube tous les soirs à 19h30 ! Découvrir la chaîne →

Triangles semblables

Se familiariser avec les triangles semblables - Exercice 3

5 min
10
COMPETENCE  :‾  Savoir  utiliser  les  notions  de  geˊomeˊtrie  plane  pour  deˊmontrer.{\color{red}\underline{COMPETENCE\;:}\;Savoir\;utiliser\;les\;notions\;de\;géométrie\;plane\;pour\;démontrer.}
Question 1
Les triangles OPROPR et STUSTU ci-dessous sont semblables.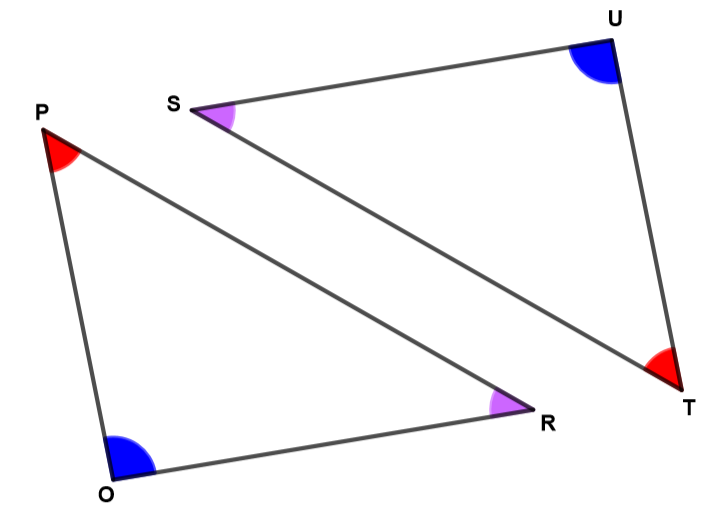

Donner les 33 paires de côtés homologues, puis en déduire l'égalité des 33 rapports correspondants.

Correction
  • Si deux triangles sont semblables alors les longueurs de leurs côtés homologues sont proportionnelles.
  • Cela signifie que les rapports (ou quotients) des longueurs des paires de côtés homologues sont égaux.
Les triangles OPR et STU sont semblables donc :.
  • Le segment [OP][OP] est homologue avec le segment [UT][UT]. (Car les angles à leurs extrémités sont de même mesure.)
  • Le segment [OR][OR] est homologue avec le segment [US][US]. (Car les angles à leurs extrémités sont de même mesure.)
  • Le segment [PR][PR] est homologue avec le segment [TS][TS]. (Car les angles à leurs extrémités sont de même mesure.)
    On peut donc en conclure l'égalité suivante :      OPUT=ORUS=PRTS\;\;\;\boxed{\red{\frac{OP}{UT}=\frac{OR}{US}=\frac{PR}{TS}}}