Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Les propriétés de la rotation - Exercice 1

10 min
25
Question 1
Le polygone RSTUVRSTUV est l'image du polygone BCDEFBCDEF par la rotation de centre EE et d'angle 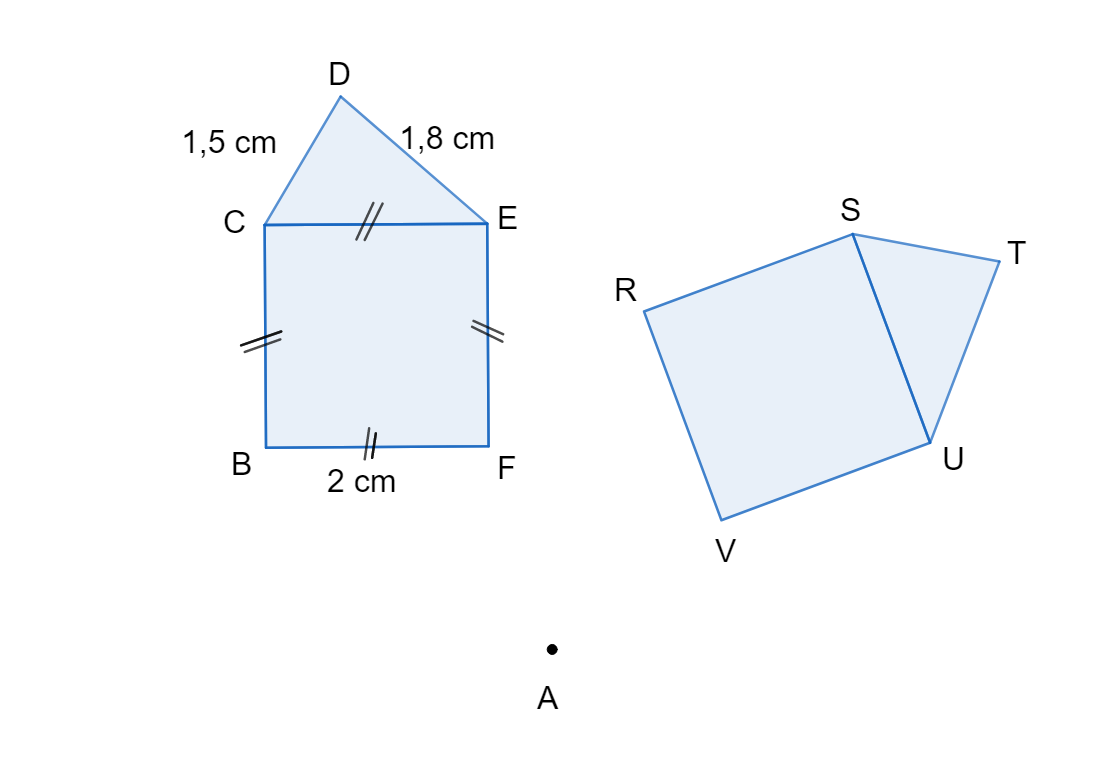70°70\degree.

Quelle est la mesure du segment [TS]  ?[TS]\;? Justifier.

Correction
    Propriétés de rotation :

    Comme la symétrie centrale, la rotation ne déforme pas les objets. La figure initiale et la figure finale sont identiques.
    Comme la symétrie centrale vu en 5eˋme,5^{ème}, la rotation conserve :
    • L’alignement des points.
    • Les longueurs des segments.
    • La mesure des angles.
    • Les aires et les périmètres.
Dans la figure ci-dessous RSTUVRSTUV, est l'image de BCDEFBCDEF par une rotation .
Or on sait que la rotation conserve les longueurs, par conséquent on en déduit donc que : TS=DC=1,5  cm.\boxed{\bf{TS= DC =1,5\;cm}}.
Question 2

Quelle est le périmètre du polygone RSTUV  ?RSTUV\;? Justifier.

Correction
    Propriétés de rotation :

    Comme la symétrie centrale, la rotation ne déforme pas les objets. La figure initiale et la figure finale sont identiques.
    Comme la symétrie centrale vu en 5eˋme,5^{ème}, la rotation conserve :
    • L’alignement des points.
    • Les longueurs des segments.
    • La mesure des angles.
    • Les aires et les périmètres.
Dans la figure ci-dessous RSTUVRSTUV, est l'image de BCDEFBCDEF par une rotation .
Or on sait que la rotation conserve les périmètres, par conséquent on en déduit donc que :
PeˊrimeˋtreBCDEF=peˊrimeˋtreRSTUVPérimètre_{BCDEF}=périmètre_{RSTUV}
Or peˊrimeˋtreBCDEF=2+2+2+1,5+1,8=9,3  cm.périmètre_{BCDEF}=2+2+2+1,5+1,8=9,3\;cm.
Donc RSTUVRSTUV a pour périmètre 9,3  cm.\boxed{\bf{9,3\;cm}}.
Question 3

Quelle est l'aire du carré RSUV  ?RSUV\;? Justifier.

Correction
    Propriétés de rotation :

    Comme la symétrie centrale, la rotation ne déforme pas les objets. La figure initiale et la figure finale sont identiques.
    Comme la symétrie centrale vu en 5eˋme,5^{ème}, la rotation conserve :
    • L’alignement des points.
    • Les longueurs des segments.
    • La mesure des angles.
    • Les aires et les périmètres.
Dans la figure ci-dessous RSTUVRSTUV, est l'image de BCDEFBCDEF par une rotation .
Or on sait que la rotation conserve les aires, par conséquent on en déduit donc que :
AireRSUV=AireBCEFAire_{RSUV}=Aire_{BCEF}
Or AireBCEF=2×2=4  cm2.Aire_{BCEF}=2\times2=4\;cm^2.
Donc BCEFBCEF a pour aire 4  cm2.\boxed{\bf{4\;cm^2}}.