Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Sujet 1 - Exercice 1

13 min
25
Question 1
Adrien veut installer chez lui un panier de basket. Il doit le fixer à 3,053,05 m du sol. L’échelle dont il se sert mesure 3,503,50 m de long.
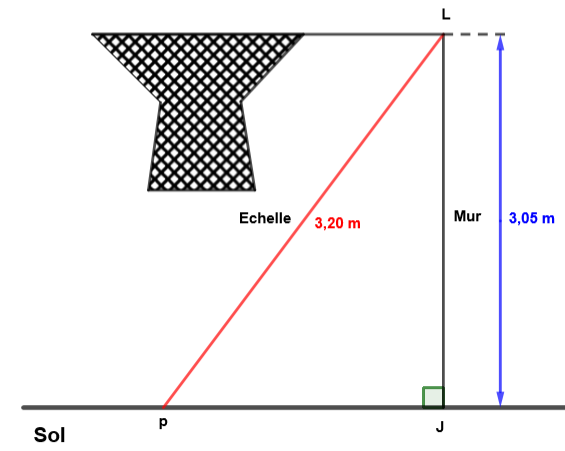
On a schématisé la situation à l'aide de la figure ci-dessous.

À quelle distance du pied du mur doit-il placer l'échelle pour que son sommet soit juste au niveau du panier ?
(Donner une valeur approchée au dixième près).

Correction
Ici, il nous faut calculer la longueur [PJ][PJ].
Comme le triangle PJLPJL est rectangle en JJ avec LJ=3,05LJ = 3,05 m et PL=3,2PL = 3,2 m. On peut appliquer le théorème de Pythagore :
PL2=PJ2+LJ2PL^{2} =PJ^{2} +LJ^{2}
  • (Le coˆteˊ que l’on recherche\text{Le côté que l'on recherche})2^{2} == (l’hypoteˊnuse\text{l'hypoténuse})2^{2} −- (le coˆteˊ que l’on connait\text{le côté que l'on connait} )2^{2}.
On a alors :
PJ2=PL2−LJ2PJ^{2} =PL^{2} -LJ^{2}
PJ2=3,22−3,052PJ^{2} =3,2^{2} -3,05^{2}
PJ2=10,24−9,3025PJ^{2} =10,24-9,3025
PJ2=0,9375PJ^{2} =0,9375. Nous allons utiliser la racine carrée pour déterminer la mesure de PJPJ.
D'où : PJ=0,9375PJ=\sqrt{0,9375}
Ainsi :
PJ=0,9682PJ= 0,9682 m

Ici, on peut convertir la longueur en cm, soit 0,96820,9682 m = 96,896,8 cm
PJ=96,8PJ= 96,8 cm

La mesure de PJPJ est donc de 96,896,8 cm. (arrondie au dixième près).
On en déduit donc que l'échelle doit être placée à 96,896,8 cm du pied du mur pour que son sommet soit juste au niveau du panier.
Question 2

Déterminer la mesure arrondie au degré près de l'angle JPL^\widehat{JPL}.

Correction
Le triangle PLJPLJ est rectangle en JJ. Nous connaissons :
  • Le côté opposé à l'angle P^\widehat{P} dont la mesure est LJ=3,05LJ=3,05 m.
  • L'hypoténuse PL=3,2PL=3,2 m.
  • Nous recherchons l'angle P^\widehat{P} .
    • Nous allons donc utiliser le sinus{\color{blue}\text{sinus}}.
    sin⁡(JPL^)=coteˊ opposeˊ aˋ l’angle P^hypoteˊnuse\sin\left(\widehat{JPL}\right)=\frac{\text{coté opposé à l'angle }\widehat{P}}{\text{hypoténuse}}
    sin⁡(JPL^)=LJPL\sin\left(\widehat{JPL}\right)=\frac{LJ}{PL}
    sin⁡(JPL^)=3,053,2\sin\left(\widehat{JPL}\right)=\frac{3,05}{3,2}
    JPL^=sin⁡−1(3,053,2)\widehat{JPL}=\sin^{-1}\left(\frac{3,05}{3,2}\right) ou encore JPL^=arcsin(3,053,2)\widehat{JPL}=\text{arcsin}\left(\frac{3,05}{3,2}\right)
    • Il faut vérifier que votre calculatrice est bien en mode degré, et n'oubliez pas de mettre les parenthèses.
    Ainsi :
    JPL^≈72,38∘\widehat{JPL}\approx72,38{}^\circ

    La mesure de l'angle JPL^\widehat{JPL} est de 72∘72{}^\circ (arrondie au degré près).