Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : 2ème partie - Exercice 3
15 min
30
Question 1
L'objectif est de calculer la hauteur d'un triangle rectangle.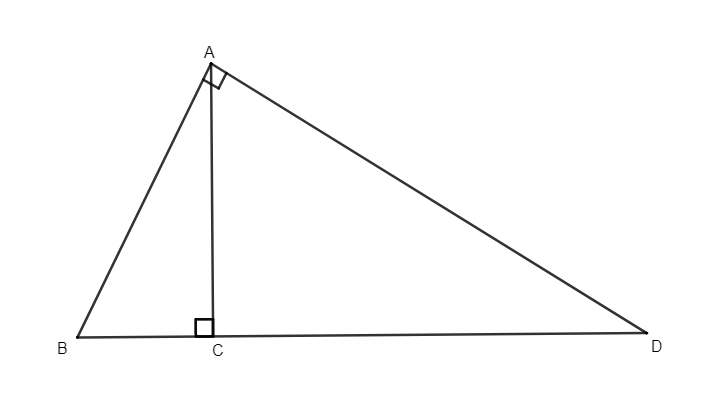

En notant , donner la mesure de l'angle en fonction de .
Correction
Dans le triangle rectangle en , on a :
et
et
Dans un triangle, la somme des angles est de .
On a donc : Question 2
Exprimer et en fonction de .
Correction
En observant la figure, on a :
Dans un triangle, la somme des angles est de .
On a donc : Question 3
En déduire que les triangles et sont semblables.
Correction
Si deux triangles ont seulement deux paires d'angles de même mesure, alors, ils sont semblables.
Des questions précédentes, on a :et
On peut donc déjà en déduire que les deux triangles ont une paire d'angles de même mesure.
Dans un second temps, on sait que les triangles et sont rectangles, par conséquent :
Dans le triangle on a : .
Dans le triangle on a : . On a donc :
On peut donc conclure que les triangles et ont deux paires d'angles de la même mesure, ils sont donc semblables.
Question 4
Montrer que
Correction
- Si deux triangles sont semblables alors le quotient des côtés homologues sont égaux.
En utilisant le produit en croix, on obtient : , on a donc :
Question 5
On a : cm et cm.
Calculer .
Correction
À la question précédente, on a déterminé l'égalité suivante :
On peut donc conclure que mesure cm.
On peut donc conclure que mesure cm.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.