Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Sujet 1 - Exercice 1

20 min
40
On donne :
  • Les points CC, DD et AA sont alignés.
  • Les points BB, EE et AA sont alignés.
  • (DE)(DE) est perpendiculaire à (AD) (AD)
  • AB=6,25AB = 6,25 ; AC=5AC = 5 ; BC=3,75BC = 3,75 ; AD=3,2AD = 3,2
  • M∈[AC]M ∈ [AC] et N∈[AB]N ∈ [AB] tels que AM=4AM = 4 et AN=5AN = 5.
    • Question 1

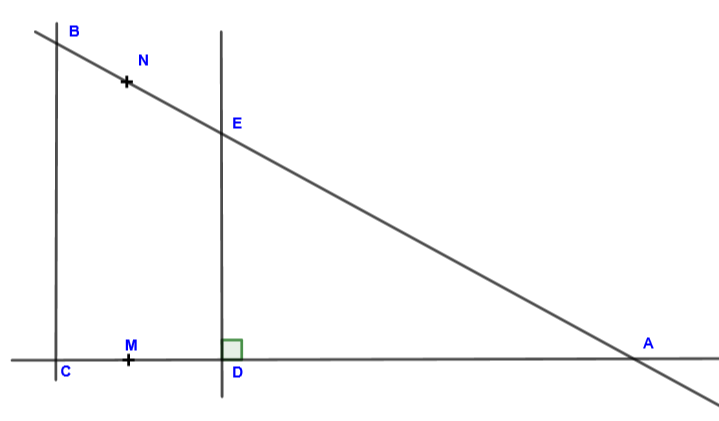
    Montrer que le triangle ABCABC est rectangle.

    Correction
    Dans le triangle ABCABC, le plus grand côté est AB=6,25AB=6,25 cm.
  • Calculons d'une part :
    • AB2=6,252AB^{2} =6,25^{2}
    AB2=39,0625AB^{2} =39,0625
  • Calculons d'autre part :
    • AC2+BC2=52+3,752AC^{2} +BC^{2} =5^{2} +3,75^{2}
    AC2+BC2=25+14,0625AC^{2} +BC^{2} =25+14,0625
    AC2+BC2=39,0625AC^{2} +BC^{2} =39,0625

    Or AB2=AC2+BC2{\color{blue}AB^{2}=AC^{2} +BC^{2}}
    Donc, d'après la réciproque du théorème de Pythagore, le triangle ABCABC est rectangle en CC.
    Question 2

    En déduire que les droites (BC)(BC) et (DE)(DE) sont parallèles.

    Correction
    Le triangle ABCABC est rectangle en CC donc (BC)⊥(AC).(BC) ⊥ (AC).
    On sait que (DE)⊥(AD)(DE) ⊥ (AD) et comme CC, DD et AA sont alignés, (DE)⊥(AC).(DE) ⊥ (AC).
    • Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles.
    Ici, on a :
  • (BC)⊥(AC)(BC) ⊥ (AC)
  • (DE)⊥(AC)(DE) ⊥ (AC)
    On peut donc en conclure que les droites (BC)(BC) et (DE)(DE) sont parallèles.
    • Question 3

    Calculer DEDE.

    Correction
  • Les points AA, EE et BB sont alignés dans le même ordre que les points AA, DD et CC .
  • Les droites (DE)\left(DE\right) et (BC)\left(BC\right) sont parallèles.
    • D'après le théorème de Thalès, on a :
    ADAC=AEAB=DEBC\frac{AD}{AC} =\frac{AE}{AB} =\frac{DE}{BC}. Nous allons remplacer par les mesures. Ainsi :
    3,25=AE6,25=DE3,75\frac{3,2}{5} =\frac{AE}{6,25} =\frac{DE}{3,75}
    À partir de 3,25=DE3,75\frac{3,2}{5} =\frac{DE}{3,75} on effectue un produit en croix. Cela nous donne :
    DE=3,2×3,755DE=\frac{3,2\times 3,75}{5}
    DE=2,4DE=2,4 cm

    La mesure du segment [DE]\left[DE\right] est de 2,42,4 cm.
    Question 4

    Les droites (MN)(MN) et (BC)(BC) sont-elles parallèles ? Justifier.

    Correction
  • Les droites (AB)(AB) et (AC)(AC) sont sécantes en AA.
  • Les points AA, NN, BB sont alignés dans le même ordre que AA, MM et CC.
    • Calculons d'une part :
    ANAB=56,25\frac{AN}{AB} =\frac{5}{6,25}
    ANAB=0,8\frac{AN}{AB} =0,8

    Calculons d'autre part :
    AMAC=45\frac{AM}{AC} =\frac{4}{5}
    AMAC=0,8\frac{AM}{AC}=0,8

    On constate ici, que : ANAB=AMAC\frac{AN}{AB}=\frac{AM}{AC}.
    Donc d’après la réciproque du théorème de Thalès, les droites (MN)\left(MN\right) et (BC)\left(BC\right) sont parallèles.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.