Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Sujet 3 - Exercice 2
6 min
10
Question 1
Le groupe des onze latinistes de la du collège a obtenu les notes suivantes à un devoir : 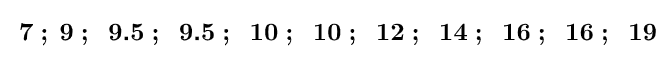
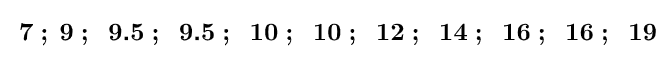
Calculer la moyenne du groupe.
Correction
La moyenne d'une série statistique est le réel, noté , tel que :
Ici, correspond à l'effectif total (le nombre total de notes), c'est-à-dire : . Il vient alors que :
.
On peut donc conclure que la note moyenne du groupe est de .
Question 2
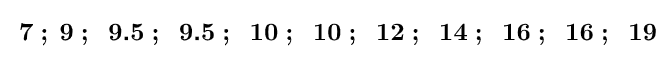
Déterminer la médiane de cette série.
Correction
Dans le cas où l'effectif total est , la médiane est la valeur ou est l'effectif total.
Ici est égal à , donc la médiane est :
termes.
termes
termes de la série statistique. Ici la valeur entourée en rouge ci-dessous.