Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 3
10 min
20
Question 1
On appelle la fonction définie par
On a utilisé un tableur pour calculer les images de différentes valeurs par cette fonction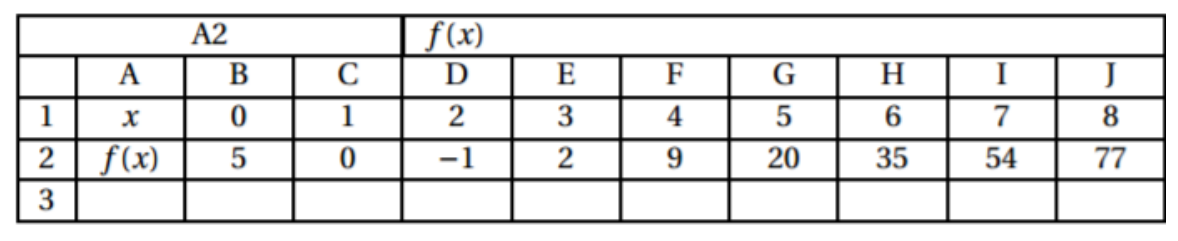
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées.
On a utilisé un tableur pour calculer les images de différentes valeurs par cette fonction

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées.
L’image de par la fonction est
Correction
Pour calculer l'image de par , il nous faut déterminer . C'est-à-dire remplacer la valeur de par . Ainsi :
Par conséquent, on peut en déduire que l'affirmation est vraie.
Question 2
Le point de coordonnées appartient à la courbe représentative de la fonction
Correction
Le point de coordonnées appartient à la courbe représentative de la fonction si l'image de par la fonction est
Autrement dit, si pour la valeur on a .
À l'aide du tableur ci-dessus, on peut en déduire que l'affirmation est vraie.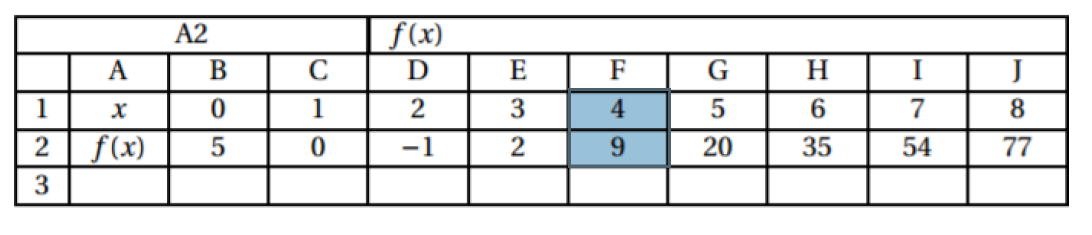
Autrement dit, si pour la valeur on a .
À l'aide du tableur ci-dessus, on peut en déduire que l'affirmation est vraie.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.